SD法詳細
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
また、表示の関係から、数式が正しく表示されていない部分があります。
以下の例の手順および数値の詳細は書籍でご確認ください。
主成分分析
互いに相関のある複数の変数からなる多変量データが得られた時、それらを、互いに独立な少数の主成分(因子)の線形結合に要約する手法である。例えば、元の変数がX1 からXp までのp個あり、それらを、p個よりも少ないm個の主成分(因子)に要約する場合、下記の式で表現できる。
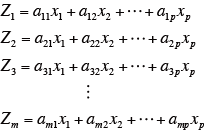
ここで、Zi は主成分(因子)得点、aji は固有ベクトルを表す。なお、主成分(因子)負荷量r(Zj, xi) は、下記のように、固有値(λ j)の平方根と固有ベクトル(aji)の積で求められる。
![]()
計算は、R などの統計ソフトで行う。主成分分析は、因子分析と同様の分析を行うものであるが、主成分分析は、因子分析のような独自性因子の想定はしていない。また、軸の回転も行わない。
事例
SD法によって地下空間に対するイメージを測定した。評価者は、地下街に勤務している一般成人50名。印象評価のための形容詞対で、左の形容詞に非常にあてはまるを1、やや当てはまるを2とし、どちらでもないを3,右の形容詞にやや当てはまるを4,非常に当てはまるを5とした。用いた形容詞は、次表にあるような16の形容詞対であった。各形容詞対に対する評価結果に基本統計量は表の通りであった。
基本統計量(件数50)

固有値、寄与率

固有値が1.0 以上の主成分は第3 主成分までだったので、第3主成分までの主成分負荷量を求める。
主成分負荷量
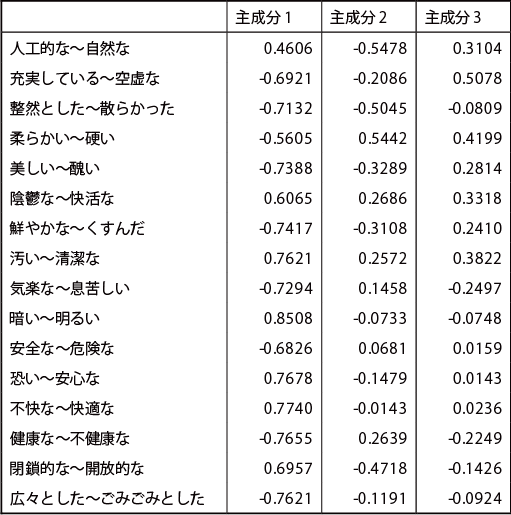
以上の主成分負荷量から各主成分を解釈すると、第1主成分の寄与率が非常に高く、50%を超えていることからも、ほとんど第1主成分だけで説明できてしまうものともいえる。主成分負荷量の絶対値が50%であり、+のものは右側の形容詞、−のものは左側の形容詞を抽出すると、第1主成分は、地下空間に対するポジティブな印象とネガティブな印象を表すものといえる。第2主成分は、人工的で硬い印象か否かを表すもの。第3主成分は、空虚な感じがするか否かを表している。
次に、評定者毎に各主成分得点を求める。
第1主成分得点の高い評定者ほど、地下空間に対してポジティブな印象を持っていることを示す。
第2主成分得点が高い評定者ほど、地下空間に対して人工的で硬い印象をもっていることを示す。
第3主成分得点が高い評定者ほど、地下空間に対して空虚な感じの印象を持っていることを示す。
主成分得点

因子分析
主成分分析と同様に、多数の変数からなるデータの次元を少数の次元に縮約する方法である。主成分分析と異なり、各変数が、それぞれの変数に共通な小数の要因(共通因子)と、その変数に固有な要因(独自因子)で構成されると想定しているところである。
因子分析モデルは、観測されるp個の変数、X1, X2,..., Xp(母平均は0と仮定する)が、それより小数のm個の変数f1, f2, …., fm(共通因子)と、Xj にのみ影響する変数ε j(独自因子)との一時結合で表されると仮定する。
![]()
ここで、係数ajk は、j番目の変数Xjのk番目の因子への負荷(ウェイト)を表しており、因子負荷量といわれる。また、ε j は、j 番目の変量に固有の独自因子である。
因子分析モデルの仮定
-
共通因子f と独自因子εは無相関
-
異なる2つの変量j, k に対応する独自因子ε j とε k は無相関
-
各変数は、共通因子f と独自因子εの線形結合で表される。
-
m 個の共通因子f1, f2, f3,・・・, fm の期待値E(fj)=0
-
独自因子のε j の期待値E( ε j)=0
-
m個の共通因子f1, f2, f3,・・・, fm で説明される分散(共通分散)をxj の分散で除した値hj2 を共通性という。0 ≦ hj2 < 1 である。
因子分析の手法としては、主因子法、最尤法、重み付き最小2乗法などがある。また、因子分析では、因子の構造を単純構造(各変数の因子負荷量が、1つの因子にだけ高い値を取り、他の因子に対しては、低い値を取るような構造)にして、因子を解釈しやすくするために、得られた因子を回転することが行われる。因子の回転法には、因子の軸の直交性を維持したまま回転する直交回転と、直交性にとらわれない、斜交回転がある。直交回転の方法もいくつかあるが、バリマックス回転が主な方法である。バリマックス回転は、各因子の分散が最大になるように回転するものである。また、斜交回転の方法としては、プロマックス回転がある。直交回転では単純構造にならない場合、斜交回転が有効になることもある。
例題
地下空間イメージ
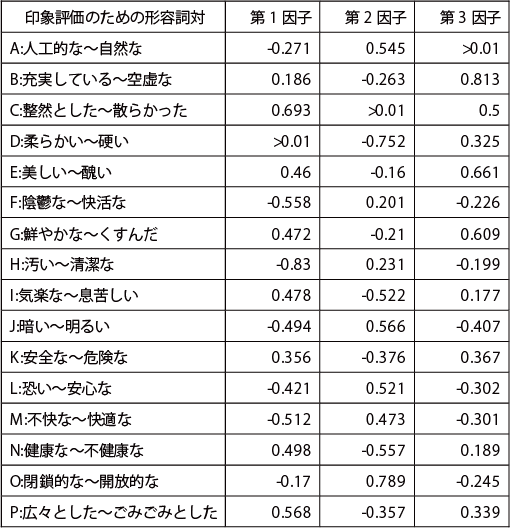
主成分分析法で用いたSD法のデータを用いた。因子数の決定は、固有値が1.0 以上の因子数で、3 因子とする(次表)。 バリマックス回転後の因子負荷量は次表の通りである。また、適合度検定結果は次表の通り。なお、適合度の検定は、最尤法、重み付き最小2乗法を行った場合に行うことができる。検定の結果p<0.01となり、1%水準でデータの分散と因子分析モデルによる推測データの分散が等しいという帰無仮説が棄却されたので、3因子では全データの分散を説明しきれなかった。因子負荷量を基に、各因子の解釈を行うと、第1因子は「散らかった」、「陰鬱な」、「不快な」、「ごみごみとした」に関連の深い因子、第2因子は「人工的な」「硬い」「息苦しい」「暗い」、「恐い」、「不健康な」、「閉鎖的な」に関連の深い因子、第3因子は「空虚な」、「醜い」、「くすんだ」に関連の深い因子といえる
次に、各評価者の因子得点の計算を行う。なお、第1因子の因子得点が高い評定者ほど、地下空間を「散らかっっていて、陰鬱で、不快で、ごみごみしている」という印象を持っている.第2因子の因子得点が低い評定者ほど、地下空間を「人工的で、硬く、不快で、恐くて、不健康で、閉鎖的」という印象を持っている.第3因子の因子得点が高い評定者ほど、地下空間を「空虚で、醜く、くすんだ」印象を持っている。因子得点の結果は、次表の通り。
因子の固有値、寄与率

バリマックス回転後の因子負荷量
適合度検定結果
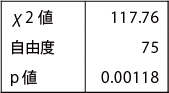
因子得点
