Rでの解析例
ここでは、順位法のページの検定をRで行います。
例題
p個の試料の順位をn人のパネルが評価したとき、あらかじめ想定した順位通りであったかどうかを検定する。
各サンプルの順位データ
| パネリスト | 試料A | 試料B | 試料C | 試料D |
| 1 | 1 | 2 | 3 | 4 |
| 2 | 2 | 1 | 4 | 3 |
| 3 | 1 | 3 | 2 | 4 |
| 4 | 2 | 1 | 3 | 4 |
| 5 | 2 | 1 | 3 | 4 |
| 6 | 3 | 1 | 2 | 4 |
| 7 | 3 | 1 | 4 | 2 |
CSVデータ作成
例題の結果を元にして、Excelを使い、以下のように集計します。
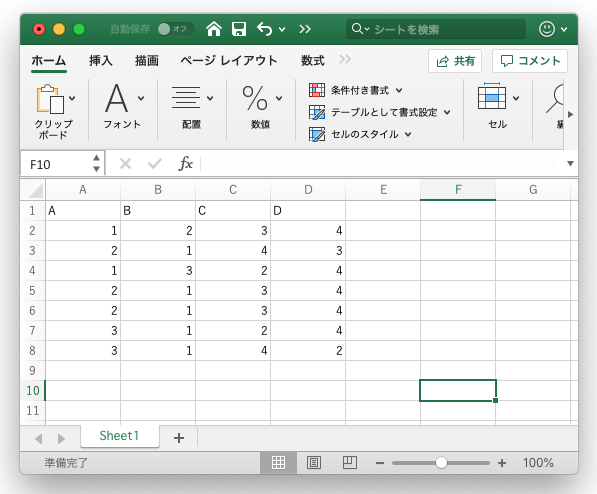
これを、csvファイルとして保存します(ファイル名はPageTestData)。保存場所はRの設定で指定した、作業フォルダです。
csvファイルはExcelを使わずに、エディタで作成しても問題ありません。
Rで解析
RStudioを起動し、コンソールに以下の順番で>の右の部分を入力します。
データファイルを読み込んでdatax に入れる
>datax <- read.csv(“PageTestData.csv”, header=TRUE)
datax の中のA に関して総和を求める
>SA <- sum(datax$A)
datax の中のB に関して総和を求める
>SB <- sum(datax$B)
datax の中のCに関して総和を求める
>SC <- sum(datax$C)
datax の中のDに関して総和を求める
>SD <- sum(datax$D)
datax の行の数を求め、p に入れる
>p <- ncol(datax)
datax の列の数を求め、j に入れる
>j <- nrow(datax)
検定のためのL を求める
>L <- SB + SA*2 + SC*3 + SD*4
L を用いて正規関数のZ 値を求め、Zを表示する。
>Z=(12*L – 3*j*p*(p+1)^2)/(p*(p+1)*sqrt(j*(p-1)))
>Z
[1] 3.404199
Z=3.404199 以上になる確率を求める
>1-pnorm(Z)
[1] 0.0003317918
得られた確率は、0.0003317918 であることから、1%の危険率で、「Γ 1= Γ 2= Γ 3=…= Γ p」とする帰無仮説は棄却され、「Γ 1< Γ 2< Γ 3<…< Γ p」とする対立仮説が採択されました。