CATA法(詳細)
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
また、表示の関係から、数式が正しく表示されていない部分があります。
以下の例の手順および数値の詳細は書籍でご確認ください。
手法
CATA法(Check-All-That-Apply)は複数の評価用語の中から試料の特徴を表すと思うものをチェックする方法で、各評価用語がチェックされた数に基づいて試料の特性を明らかにしようとするものである。一般に、CATA法では同じパネリストがすべての試料を評価する。試料間で各評価用語がチェックされた度数に統計的に有意な差があるかどうかを、コクランのQ検定により検定する。同じパネリストがすべての試料を評価するので、対応のあるデータになる。そのためにχ2検定を行うことはできない。
例
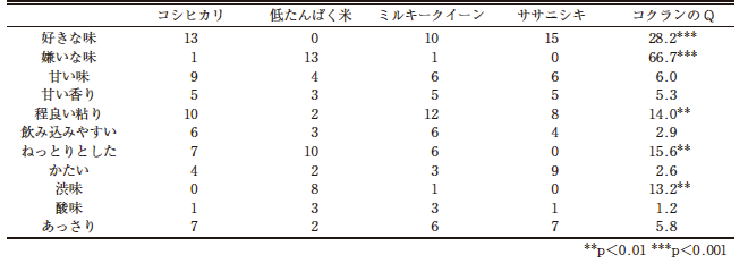
表にCATA 法を用いて4種類の炊飯米(コシヒカリ、低たんぱく米、ミルキークイーン、ササニシキ)を「好きな味」から「あっさり」まで11 の評価語について評価した時の結果の一例を示す(島村等,2017)。
チェックリスト表

CATA 法結果(好きな味:一部) (市原,2018)

なお,図は、チェックリスト表の例である。表は、評価用語の中の「好きな味」にチェックを入れたかどうかを示しており、チェックを入れた場合には1を、入れなかった場合には0 が記録されている。この表からも明らかなように,一人のパネリストがすべての試料を評価しているので,χ2検定ではなく,コクランのQ 検定を行い、「好きな味」という評価用語がチェックされる度数が試料間で異なっているといえるかどうかを検定する(同様の検定は,他のすべての評価用語についても行うものとする)。
次に、評価用語毎に4種類の炊飯米がチェックされた度数を求め(表)、そのデータを基に対応分析を行い、少ない次元で各評価語と各炊飯米の関係を探ることにする。
コクランのQ 検定
表を基に,検定統計量Qを式により求める。
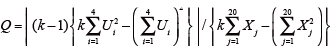
この例では,
![]()
となり、これをχ2値として検定する。なお、自由度df は、df=k-1=3である。巻末のχ2表より、自由度3で危険率0.1%のχ2値は16.3 で、求めたχ2値28.2 はそれよりも大きな値であったので、本例では,危険率0.1%で試料間に有意差があるといえる。
同様の検定をすべての評価語に対して行った結果は,次表に示すとおりである。
CATA 法による各評価用語の選択度数と検定結果
対応分析
対応分析は,カテゴリカルデータの解析方法の一つで、数量化Ⅲ類や双対尺度法と同じ仲間に入るものである。対応分析の基本は、行(例えば試料)と列(例えば評価用語)からなる分割表で行の項目と列の項目の相関が最大になるように行と列を並び替えることである。その意味で、主成分分析や因子分析と考え方は同じといえる。ただし、主成分分析や因子分析が連続量のデータを扱うのに対し、対応分析はカテゴリデータを扱う点で異なっている。対応分析の解析は、コンピュータのソフトの利用なしには実現できないが、Rによる解析方法も公開されている。
例
前表のCATA法で得られた度数表を用いて対応分析を行った結果の例を図に示す。ササニシキの近くに「かたい」の評価用語が位置し、低たんぱく米の近くには「嫌いな味」「渋味」が、ミルキークイーンとコシヒカリは近くに位置し、「ほどよい粘り」「飲み込みやすい」などの評価用語が位置している。
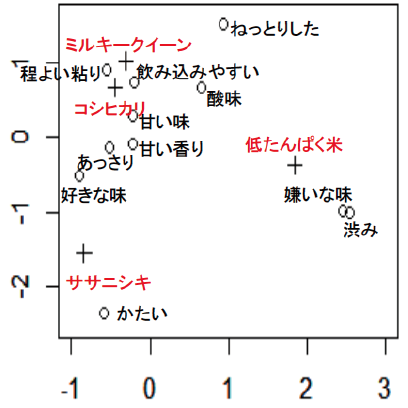
対応分析の結果 ○:評価用語 +:試料