2点試験法
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表は省略しています。
また、表示の関係から、数式が正しく表示されていない部分があります。
以下の例の手順および数値の詳細は書籍でご確認ください。
手法
あらかじめ客観的な順位がついている2種の試料間の差をパネリストが識別する能力を持つか否かを検定する際に用いる。2つの試料を同時、または、継時的に示し、どちらの試料の強度が強いかを判定させ、その正答率を測定する。一人のパネリストがn回識別試験を行う場合とn人のパネリストが1回ずつ識別試験をおこなう場合とがある。片側検定を用いる。
例
パネリストにAとBの内、どちらの試料の強度が強いか(A かB)を答えてもらう。
帰無仮説:パネリストはAとBを識別する能力を持たない。
n回中、k回正答で、n-k 回誤った時、その確率は、
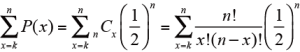
となる。
例えば、10回中9回正答し、1回誤答した場合。
上式より、その確率は、p(10)+p(9) となる。
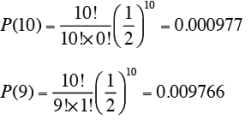
より、
P(9)+P(10)=0.009766+0.000977=0.010743
となり、5%(0.05)よりも小さな値になることから、危険率5% で、パネリストがAとBを識別できないとする帰無仮説は棄却され、パネリストは、AとBを識別できるといえる。
また、10 回中、8 回正答で、2 回誤った時、
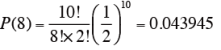
P(8)+P(9)+P(10)=0.043945+0.009766+0.000977=0.054688 (>0.05) となり、0.05 よりも大きな値になることから、5%水準で有意でない、つまり、帰無仮説を棄却できない:パネリストはAとBを識別できないことになる。
n>100 の時は、次式により、正規分布近似を行ない検定する。
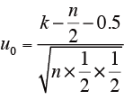
u0 ≧ u αならば、帰無仮説を棄却する。
α =0.05 の時、u0.05=1.64485
α =0.01 の時、u0.01=2.32635
事例
試料Aと試料Bの2種類の苦み成分量の異なるポテトチップを用意する。なお、ここでは、試料Bの方が苦みが強いものとする。20 人のパネルがそれぞれ1 回ずつ両者を比較し、どちらが試料Bか(どちらが苦いか)を答える。試料Bの方が試料Aよりも苦いと答えたパネルは、20 名中17 名であった時、これらのパネルは、試料Aと試料Bの苦みを識別できたといえるか。
考え方:p の計算は、上記の方法により直接求めるか、あるいは、検定表(略)により行う方法がある。
今回は、n=20,k=17 である。片側検定を行う。