2点嗜好法
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表は省略しています。
また、表示の関係から、数式が正しく表示されていない部分があります。
以下の例の手順および数値の詳細は書籍でご確認ください。
手法
2種の試料に対する嗜好や良否に有意な差があるかどうかを検定する際に用いる。2つの試料(例えば、AとB)を同時、または、継時的に示し、どちらの試料を好むかを判定させ、その回答率を測定する。n人のパネリストが1回ずつ判定を行う。両側検定を用いる。
例
試行数(パネリストの人数)をn、Aの方を好むと回答した数とBの方を好むと回答した数の内、度数の多い方をkとする。
帰無仮説:パネリストのAとBに対する嗜好に差はない。
n人の内、k人だけAまたはBを選ぶ確率は(x ≠ k)、
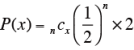
n人の内、k人がAまたはBを選ぶ確率は、
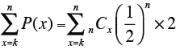
となる。
そこで、例えば、10人の内、9人がAまたはBを選ぶ確率は、{P(10)+P(9)}× 2 となる。
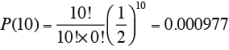
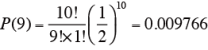
であることから、
{P(9)+P(10)} × 2={0.009766+0.000977} × 2=0.021494
と、0.05 以下であることから、5%水準で有意となり、パネリストのAとBに対する嗜好に差はないとする帰無仮説を棄却する(嗜好に差がある)ことになる。10 人の内、8人がAまたはBを選ぶ場合には、その確率は、{P(8)+P(9)+P(10)} × 2 で求められ、
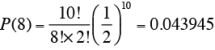
であることから、{P(8)+P(9)+P(10)} × 2={0.043945+0.009766+0.000977} × 2=0.109376 (>0.05) となる。
よって、 5%水準で有意でない(帰無仮説を棄却できない、つまり、AとBに対する嗜好に差はない) ことになる。
n ≦ 100 の時は、上記のように直接確率を計算する方法の他に、検定表(略)を利用する方法もある。
n>100 の時は、次式により、正規分布近似を行ない検定する。
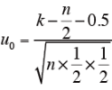
u0>=uαならば、帰無仮説を棄却する。
α =0.05 の時、u0.025=1.95996
α =0.01 の時、u0.005=2.57583
事例
90 人の消費者パネルに軽自動車AとBの後部座席の乗り心地の評価をしてもらったところ、そのうち60人のパネルが、Aの方が乗り心地が良いと答えた。Aの方が後部座席の乗り心地が良いと考えて良いであろうか。
考え方
2 点嗜好法は両側検定である。検定表より、n=90 で危険率5%の棄却限界値は、55、危険率1%の棄却限界値は、58、危険率0.1%の棄却限界値は、61、なので、危険率1% で、Aの方が後部座席の乗り心地が良いといえる。
n>100 の場合は、すでに述べた式により正規分布近似を行ない検定する。