配偶法
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
手法
t個からなる試料の組みを2組作る。パネリストには、第1組の1つの試料と同じと思われる試料を第2組から選択するということを行ない、最終的に、t対の組み合わせを作る課題を行なわせる。t対の組み合わせの内、何対正解したかということで、パネリストの識別能力を測定することができる。
なお、1人のパネリストに1回のみの判定で繰り返しを行なわない場合と、繰り返しを行なう場合とがある。
また、試料の組みを作る際に、t個とt個というように同数の組みにして揃える場合と、t個と(t+1)個、あるいは、(t+2)個というように同数にしない場合とがある。
解析
帰無仮説は、t個の試料が区別できないである。
t個の試料が区別できなくて、その結果ランダムに対をつくるとすると、t対のうちs対がちょうど正しく組み合わされる確率は、
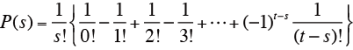
で与えられる。
この式を用いて、s対だけでなく、s対以上が正しく組み合わされる確率をすべて加算する。その確率が、α(例えば、5%)以下であれば、有意水準αで帰無仮説は棄却され、t個の試料の区別ができることになる。なお、この式は、t が4以上になると急速に収束するので、試料の数が4以上(t ≧ 4)の場合、その確率は、tとは無関係に決まってしまう。
数表(略)では上記の確率が5%以下であるようなs が示されている。なお、この表において、t(試料の数)は4 以上で、nは繰り返し数である。正しく組み合わされた数、または、平均値が表の値s 以上であれば、危険率5%で有意となる。
t個同士のマッチングで繰り返しのない場合
手順
互いに相異なるt種類(t≧4)の試料を2 組用意する。次に、一人のパネリストに、同種の試料が2 組用意してあることを知らせ、各組から1個ずつ取り出して同種の試料の組み合わせを作らせる。
- 正しい組み合わせの数s を数える。
-
数表(略)より繰り返し1回(n=1)の時のs の値よりも、sが大きな値をとったばあいには(s ≧4であれば)、5%水準で有意である。
例
パネリストの色相の識別能力を判定するために、色相がわずかに異なるA,B,C,D,E,F の6種類の色票を2組作る。それぞれのパネリストに、同種の試料が2 組用意してあることを知らせ、各組から1個ずつ取り出して同種の試料の組み合わせを作らせる。
判定:正しい組み合わせの数、sを数え、s ≧4であれば、5%水準で有意である。

データ例
t個同士のマッチングで繰返しのある場合
例
3人のパネリストに繰り返して実施した場合。(一人のパネリストが3回繰り返す場合も可)

- 正しい組み合わせの数sを数える。
- 正しい組み合わせの数sの平均Save を求める。この例では、Save=(3+4+4)/3=3.67
- 繰り返しnの時のSave が、検定表の値以上であれば、5%水準で有意。この場合は、Save がn=3 の時の値2.33 よりも大きな値だったので、5%水準で有意。
t個と(t+1)または(t+2)個のマッチングの場合
1組はt個、もう1組は(t+1)または(t+2)個を用意する。パネリストには、同種の試料が用意してあることを知らせ、各組から1 個ずつ取り出して同種の試料の組み合わせを作らせる。なお、t 個とu 個(u>t)のマッチングを行ったときのp(s) は、以下の式で求められる。
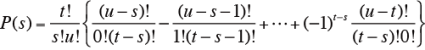
この式を用いて、s対だけでなく、s対以上が正しく組み合わされる確率をすべて加算する。その確率が、α(例えば、5%)以下であれば、有意水準αで帰無仮説は棄却され、t個の試料の区別ができることになる。検定表(略)は、上記の確率が5%以下であるようなsが示されている。なお、この表において、t(試料の数)は4 以上で、nは繰り返し数である。正しく組み合わされた数、または、平均値が表の値s以上であれば、危険率5%で有意となる。
例
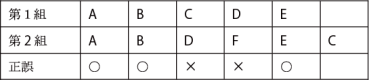
- 正しい組み合わせの数sを数える:s= 3
- 検定表からt=5の時の(t+1)個とのマッチングの限界値を読み取る:この場合、限界値は3なので、5%水準で有意。
- 結果、このパネリストは試料の識別能力があるといえる。