格付け法
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
また、表示の関係から、数式が正しく表示されていない部分があります。
J-SEMS.PROで以下の解析を行うことができます。
手法
試料を特級、1級、2級へ分類したり、良品、不良品に分類したりする方法で、順序尺度への分類として処理されることが多く、クロス表によるχ2検定を行なうのが一般的である。
格付け法は、点数で処理されるために、採点法と似ているように感じるかもしれないが、格付け法の場合は、得られたデータは順序尺度のデータであるのに対し、採点法の場合は、間隔尺度のデータであるため、異なる解析方法をとることになる。
格付け法は、独立評価を用いるので、評価者が試料の識別能力を十分に有していないと、データが不安定になり、他の選別試験の結果と異なる結果になることもある。評価者の能力と判定基準の学習が必要な測定法ともいえる。これは、採点法にも当てはまることである。
採点法の場合は、評点が等間隔性を有するようにという縛りがあるため、格付け法に較べると、評価者はむずかしい判断をしなくてはならないことになる。量的な判断がむずかしく、順位の判断ならば安定した回答が引き出せそうということであれば、採点法よりも格付け法を用いた方がよい。その場合には、データは、順序尺度になるので、統計的な解析は、ノンパラメトリックな方法になり、採点法のデータよりも解析は若干制約を受けることになる。
すでに述べたように、格付け法の評価結果が、試料間で異なるかどうかを検定するためには、χ2検定を用いるが、χ2検定は,対応のない2群以上の比率の検定を行うときに用いる方法であることに留意する必要がある。同じパネルがすべての条件を評定するような対応するデータの場合は、コクランのQ 検定などを用いる必要がある。2×2のクロス表の分析で,セルの期待値が5未満になるものがあったら,χ2検定を行うのは適切ではない.その場合には,フィッシャーの直接確率法を行う.また、2×3以上のクロス表の場合には,期待値が5未満のものが全体の20%以上あるか,1未満の期待値が1つでもある場合は,χ2検定は適切ではない.その場合は,2つ以上のカテゴリ−を一つに統してからχ2検定を行う。
実例
200人のパネルを50人ずつの4グループに分け、各グループに、A,B,C,Dの4つの試料のいずれかを割り当て、それぞれ上、中、下の3 段階で評価してもらった。A,B,C,Dによって、差があるといえるか。
実験者用記録用紙の例

分析
クロス(分割)表によるχ 2 検定
-
検査結果 度数表(分割表:実測値Oij)
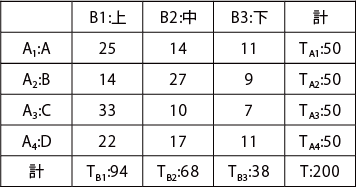
-
各級の期待値(Eij)を求める。
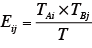
各級の期待値(Eij)

-
実測値Oij と期待値Eij との差(Oij − Eij)を求める。
実測値Oij と期待値Eij との差(Oij − Eij)

-
偏差の2 乗を計算する。
実測値Oij と期待値Eij との差の平方 (Oij − Eij)2
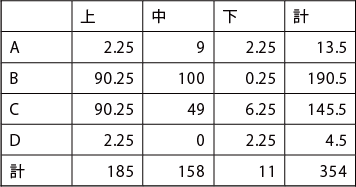
-
χ 2 値を求める。
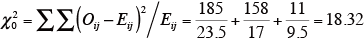
-
自由度df を求める。
df=(A の水準数−1) ×(Bの水準数−1)
df = (4 − 1) × (3 − 1) = 6 -
検定する。
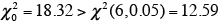
よって、5%水準で有意(significant)である。(求めたχ 02 値が、対応するχ 2 よりも低い値であれば、有意ではない)