採点法
0〜3,1〜5,−3〜+3などの数値尺度を使って、試料の特性や好ましさに対して評点を与える手法です。数値間の心理的間隔が等しくなるように、つまり、カテゴリーの幅が一定となるように判断することがパネリストに要求されます。
J-SEMSで実施できる採点法と解析は以下です。
| 解析方法 | 概要 |
| 対応のあるデータの場合 | 複数のパネリストが2つの試料を採点します。各パネリストは両方の試料を採点します。 |
| 対応のないデータの場合 | 複数のパネリストを2つのグループに分け、2つの試料を採点します。各パネリストはどちらかの試料を採点します。 |
| 一元配置の分散分析 | 複数の試料を複数のグループのパネリストに採点させ(各グループは1つの試料を採点する)、各試料の採点に差があるかを調べる。 |
| 二元配置の分散分析 | 複数の試料を複数のパネリストが採点法によって評価した場合の解析方法です。繰り返し有り無し、つり合い不完備型ブロック計画で解析方法が異なります。 |
| 積率相関 | 複数の試料を2人のパネリストが採点法で評価し、パネリスト間の関係を調べます。 |
| 単回帰分析 | 複数の試料を複数のパネリストが評価した時、試料の評価が直線的であるかを調べます。 |
| 重回帰分析 | 複数の試料を複数のパネリストが複数の要因について採点した時、主たる要因とその他との関連性を調べます。 |
| 判断分析 | 複数のグループのパネリストが複数の試料を採点した時、採点結果とグループの関連性を調べます。 |
1.対応のあるデータの場合
例
 |
10人のパネリストに2種類のカメラの品質について10点満点で採点した。その際、5人は、Aを先に、残りの5人は、Bを先に評定して、順序効果が出ないようにした。各カメラの平均評定値に差があるといえるかを調べる。 |
説明
2つの試料に対する評定値の平均に差があるかどうかを検定する場合t 検定を用います。
J-SEMS 試験解析画面


さらに詳しく
ガイドブック「製品開発に役立つ感性・官能評価データ解析-Rを利用して-」での解説
2.対応のないデータの場合
例
 |
各10名からなる2群のパネルの一方にはA,他方にはBの中華まんを提示し、その品質の良さを1点(不良)〜10点(良)の採点法で評価させた。 |
説明
2群の母標準偏差が等しいことをF検定により、確認します。
J-SEMS 試験解析画面


さらに詳しく
ガイドブック「製品開発に役立つ感性・官能評価データ解析-Rを利用して-」での解説
3.一元配置の分散分析
例
 |
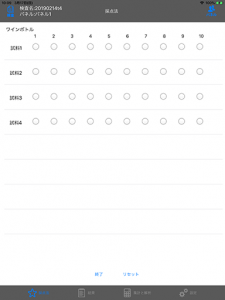
ワインのパッケージデザインの試作品が4つある。これらの試作品の良さを、10点満点の採点法で各試料4名ずつが評定した時、以下の表のような結果を得た。4つのパッケージデザインに対する評定値に差があるといえるか。また、差があった場合、どのパッケージ間に差があるか。 |
説明
3つ以上の試料に対する評価についての母集団の平均値に差はないという帰無仮説を検定する場合に用います。例えば、4つの試料に関して調べるとき、その中の一つの試料に対する評価値は、4つの試料の平均評価値からのずれ(群間のずれ)とその試料の平均からのずれ(群内のずれ)に分解できます。群間のずれは、試料の性質の違いによって生じるずれであるのに対し、群内のずれは、同一の試料内で生じるものであり、誤差によって生じると考えられます。そこで、群間と群内のずれの大きさを比較し、群内のずれの大きさ(誤差)に較べて、群間のずれの大きさが相対的に大きければ、試料の性質の違いが測定値の違いとしてあらわれたことを示すものと考えようというのが分散分析の基本的な考え方です。
J-SEMS 試験解析画面

さらに詳しく
ガイドブック「製品開発に役立つ感性・官能評価データ解析-Rを利用して-」での解説
4.二元配置の分散分析(繰り返しなし)
例
 |
10点満点の採点法で、3人のパネリストが3種類の焼酎を評価した。焼酎とパネリスト及び交互作用には、有意な効果があるかを調べる。 |
説明
要因が2つ(例えば、試料の違いの要因と評価者の違いの要因)あったときに、それらの要因がデータに及ぼす効果について検定します。
J-SEMS 試験解析画面


さらに詳しく
ガイドブック「製品開発に役立つ感性・官能評価データ解析-Rを利用して-」での解説
5.二元配置の分散分析(つり合い不完備型ブロック計画)
例
 |
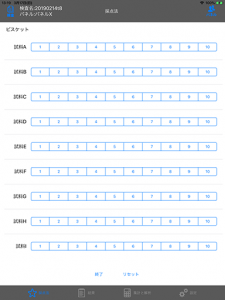
4種類のウィスキーを10人のパネリストが7段階で採点する。各パネリストは3つの試料を評価する。 |
J-SEMS 試験解析画面


さらに詳しく
ガイドブック「製品開発に役立つ感性・官能評価データ解析-Rを利用して-」での解説
6.積率相関
例
 |
XとYの2名の評価者に試料A~Iの品質の良さについて10点(良)~1点(不良)の採点法を用いて採点した。2名の評価者の関係について調べる。 |
説明
間隔尺度以上の2組のデータの線形関係の強さや、その方向を示す測度で、-1から1の間の値をとります。
- 一方が増加したときに、他方も増加する関係があるとき、正の相関があるといい、相関係数r>0となります。
- 一方が増加したとき、他方が減少する関係があるとき、負の相関があるといい、相関係数r<0となります。
- 一方の増加や減少と、他方の増加や減少との間に、まったく関連性が見られないとき、相関がないといい、相関係数r=0となります。
J-SEMS 試験解析画面

さらに詳しく
ガイドブック「製品開発に役立つ感性・官能評価データ解析-Rを利用して-」での解説
7.単回帰分析
例
 |
8種類の婦人靴を履いて長時間作業をした時の疲労度について、20名の評定者に7段階の採点法で評価してもらい、その平均値を求め、それぞれの靴のヒールの高さとの関連を調べた。 |
説明
事前に得られるいくつかの情報(X1,X2,X3,…)から、ある事象Y を予測するのが、回帰分析です。官能評価の場合、様々な変数が、試料に対する嗜好評価やその他の官能量と関係しています。それらの変数が、嗜好の度合いをどれくらい予測できるのかを問題にするとき、用いられるのが、回帰分析である。Yは、嗜好の度合いなどの官能量になる。Xが一つの場合には、単回帰分析になり、二つ以上になると重回帰分析になります。ここで、Xは、独立変数とか説明変数、あるいは、予測変数と呼ばれ、Yは、従属変数とか目的変数と呼ばれている。
J-SEMS 試験解析画面


さらに詳しく
ガイドブック「製品開発に役立つ感性・官能評価データ解析-Rを利用して-」での解説
8.重回帰分析
例
 |
オレンジジュースの甘味と酸味の主観的な強度が、イチゴのおいしさの評価に与える影響を調べるために、20人のパネルに10種類のオレンジジュースを7段階の採点法で評価してもらった。オレンジジュースの甘味と酸味の主観量で、おいしさの主観量が予測可能か否かを検討する。 |
説明
2つ以上の説明変数(X1,X2,X3,…)が目的変数y に及ぼす影響の強さや予測力を測定します。重回帰分析では、複数個の独立変数xi (i ≧ 2) と、従属変数y の間に、以下の一次式のような関係を考え、偏回帰係数b や定数a を求めるとともに、重回帰式の予測の精度を評価します。また、重回帰分析では、独立変数を固定して分析する方法(全投入法)と、独立変数を増減させて分析することで、最善の独立変数を決定するステップワイズ法があります。
J-SEMS 試験解析画面


さらに詳しく
ガイドブック「製品開発に役立つ感性・官能評価データ解析-Rを利用して-」での解説
9.判断分析
例
 |
20代と60代の男性に3種類のスーツに対する好みの度合いを採点法で評価してもらった結果である。これら3種類のスーツに対する好みから、年代を判別することが可能かを線形判別法で調べる。 |
説明
回帰分析は目的変数が数量(間隔尺度以上)でしたが、判別分析法は、目的変数がカテゴリーの場合に、適用されます。例えば、A群とB群に所属するデータ群が、それぞれ2 変量X1 とX2 の値を持ち、X1 とX2 の二次元の座標上にプロットされたとします。この時、A群のデータをB群に誤判別したり、B群のデータをA群に誤判別する確率を最小にする分析方法を判別分析といいます。
J-SEMS 試験解析画面


さらに詳しく
ガイドブック「製品開発に役立つ感性・官能評価データ解析-Rを利用して-」での解説