平均値の差の検定(t検定)
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
また、表示の関係から、数式が正しく表示されていない部分があります。
J-SEMS.PROで以下の解析を行うことができます。
概要
2つの試料に対する評定値の平均に差があるかどうかを検定する場合t 検定を用いる。パネリストは2群に分かれ、それぞれ異なる試料を評価したり(対応のあるデータ)、同一のパネリストが、それぞれ異なる試料を評価する場合もある(対応のないデータ)。2群の母標準偏差が等しい場合と等しくない場合、同一のパネリストが2つの試料を評価する(対をなすデータ)場合で、検定法がそれぞれ異なる。
対応のあるデータの場合
例
10人のパネリストに製品AとBの品質について、採点法により評定させた。なお、その際、5人は、Aを先に、残りの5 人は、Bを先に評定して、順序効果が出ないようにした。なお、尺度は、1点から10点の10段階スケールであった。製品AとBの平均評定値に差があるといえるか。
採点法による対応のあるデータの例

-
表に示すようにdi= XA-XBを求める。
- dの平均値を求める。
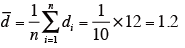
この例では、n=10 -
次式によってSd2 を求める。
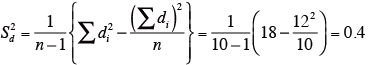
-
次式によってt0 を求める。
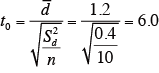
検定
両側検定の時、|t0| ≧ t(n − 1, α /2) ならば、危険率αで、有意差有り。
片側検定の時は、|t0| ≧ t(n − 1, α ) ならば、有意差有り。
この例では、両側検定を適用するので、両側検定で危険率αに相当するt0 値をt表(略)より求める。危険率α =0.01、df=9 のt 値は、3.250 となることから、この例では、|t0| = 6.0>3.250 となり、1%水準で有意。よって、試料AとBに対する評定値は危険率1%水準で有意差がある。
対応のないデータで、等分散の場合
対応のないデータの場合(パネリストを2群に分けて、それぞれ異なる試料を評価する場合)は、まず、2つの標本間の等分散の検定を行なう:つまり、2群の母標準偏差が等しいことをF検定により、確認する。
例
各10 名からなる2群のパネルの一方にはA,他方にはBの製品を提示し、その品質の良さを1点(不良)〜10点(良)の採点法で評価させた。以下の表ようなデータが得られたとき、AとBの間に品質の差があるといえるか。
採点法による対応がなく等分散のデータの例
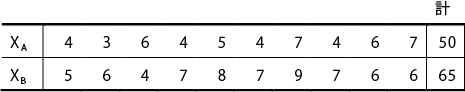
上記のデータ表をExcel に入力して、F検定をする。なお、F値を求めるときは、分散が大きい方が分子となる。この例では、XAの不偏分散σA 2 は、Excel 関数VARより、2、XB の不偏分散σB 2 は、2.056 である。よって、F 値は、
![]()
となる。その結果、dfB(分子の自由度)= nB- 1=9、dfA(分母の自由度)=nA – 1=9、F0=1.028、なので、F 表(略)よりp>0.05 となり、帰無仮説は捨てられない(有意ではない)。そこで、両者は、等分散として扱うことにし、2群の母標準偏差が等しい場合(等分散の場合)の検定をする。
t値を下記の式により求め、t検定する。
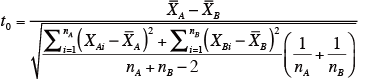
あるいは、
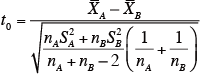
ただし、
nA:製品A の評価数(標本数)
nB:製品B の評価数(標本数)
XA :製品A の平均評定値
XB :製品B の平均評定値
SA2:製品A の標本分散
SB2:製品B の標本分散
両側検定の場合、|t0 | ≧ t(df, α /2) ならば、危険率αで有意。
片側検定の場合、|t0 | ≧ t(df, α ) ならば、危険率αで有意。
結果:
各群の人数:
nA=10
nB=10
試料A の平均評定値:5
試料A の評定値の標本分散:1.80
試料B の平均評定値:6.5
試料B の評定値の標本分散:1.85
よりt0=2.36
自由度 df=nA+nB-2=18
今回は、両側検定を採用する。α =0.05、自由度df=18 の時のt値を求めると、t=2.101 になる。t0 ≧ t より、AとBは、5%水準の危険率で有意差があるといえる。
対応のないデータで、等分散でない場合
対応のないデータの場合(パネリストを2群に分けて、それぞれ異なる試料を評価する場合)は、まず、2つの標本間の等分散の検定を行なう:つまり、2群の母標準偏差が等しくないことをF検定により、確認する。
例
20人のパネリストをランダムに2群に分け、一方の組にはA,他方にはBの製品の品質の良さを1点(不良)〜10点(良)の採点法で評価させた。以下の表ようなデータが得られたとき、AとBの間に品質の差があるといえるか。
採点法による対応がなく、等分散でないデータの例
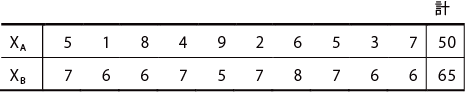
はじめに、F検定を行い、2 群が等分散か否かを検定する。次にt 検定を行う。検定の種類に関しては、Excel で行う場合、F検定の結果、2群の母標準偏差が等しい場合は2を、2群の母標準偏差が等しくない場合は、3を入力する。
F検定による等分散の確認
上記の例では、XA の分散VA は6.67、XB の分散VB は0.72 になる。その結果、F0=VA/VB=6.67/0.72=9.23 となる。なお、F0 を求める際には、分散の小さいものを分母にし、大きいものを分子にする。
dfA(分子の自由度)= nA − 1=9
dfB(分母の自由度)= nB − 1=9
F0=9.23
より、危険率を求めると、p=0.001 となる。
この結果、危険率p は0.05 よりも小さいために、有意となり、両群の分散は等分散ではないことから、ウェルチの検定を行う。

ただし、
nA:製品A の評価数(標本数)
nB:製品B の評価数(標本数)
XA :製品A の平均評定値
XB :製品B の平均評定値
σA 2 :製品A の不偏分散
σB 2 :製品B の不偏分散
また、自由度df は、下記の式により求める。
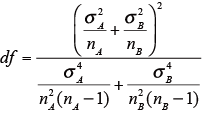
両側検定の場合:|t0 |≥t(nA+nB2, α /2) ならば、危険率αでH0 を捨てる(有意)。
片側検定の場合:|t0 |≥t(nA+nB2, α ) ならば、危険率αでH0 を捨てる(有意)。
なお、今回は両側検定を用いる。
結果
試料A 平均評定値XA :5
不偏分散σA 2 :6.67
試料B 平均評定値XB :6.5
不偏分散σB 2 :0.72
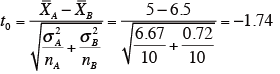
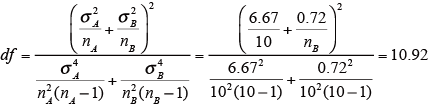
となる。両側検定で危険率5% のt値は、t 表(略)では自由度が10.92 以上で1番近い自由度11 のt 値で、t(11,0.05)=2.201 である。
|t0|=1.74 < 2.201 より、AとBは、有意差がないといえる。
t 検定をする前に、F 検定をして母標準偏差が等しいかどうか(等分散かどうか)を検定することによってウェルチの方法を用いるか否かを判断することが行われているが、F検定をしてからt 検定をするというように検定を繰り返すことは、よくないという考えもある。この問題を解決する方法として、2段階の検定をせずに、はじめからウェルチの方法を使うという方法も提唱されている。