回帰分析
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
また、表示の関係から、数式が正しく表示されていない部分があります。
J-SEMS.PROで以下の解析を行うことができます。
手法
事前に得られるいくつかの情報(X1,X2,X3,…)から、ある事象Y を予測するのが、回帰分析である。官能評価の場合、様々な変数が、試料に対する嗜好評価やその他の官能量と関係している。それらの変数が、嗜好の度合いをどれくらい予測できるのかを問題にするとき、用いられるのが、回帰分析である。Yは、嗜好の度合いなどの官能量になる。Xが一つの場合には、単回帰分析になり、二つ以上になると重回帰分析になる。ここで、Xは、独立変数とか説明変数、あるいは、予測変数と呼ばれ、Yは、従属変数とか目的変数と呼ばれている。
単回帰分析
説明変数または独立変数(x で表す) の値を固定したとき、結果となるべき特性(目的変数または従属変数(yで表す) の期待値ˆyとxとの間にˆy = ax + b という直線的な関係が成立するかどうかを分析する。a及びbは、予測値ˆy と、実測値y の差の二乗和が細小になる値で、最小二乗法によって求める。つまり、
![]()
が最小になるようなa とb を求める。
aとbは、下記のような一般式によって求めることができる。
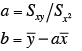
例
8種類の婦人靴を履いて長時間作業をした時の疲労度について、20名の評定者に7 段階の採点法で評価してもらい、その平均値を求め、それぞれの靴のヒールの高さとの関連を調べたところ、次表のようになった。
ヒールの高さと疲労度(単回帰分析のためのサンプルデータ)
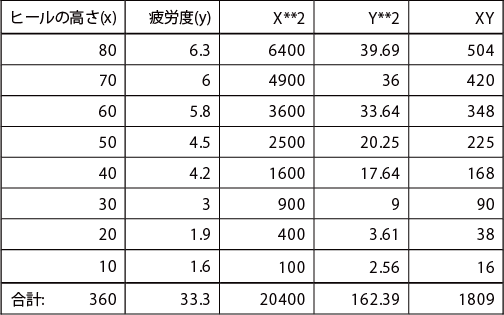
靴のヒールの高さと疲労度の平均評価値との間の関連性を見るために、ヒールの高さを説明変数(x)、疲労度を目的変数(y)とした単回帰分析を行う。
平均:
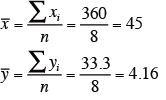
偏差平方和:
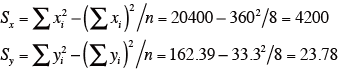
偏差積和:
![]()
回帰係数:
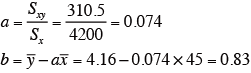
したがって回帰式は、
![]()
となる。
また、決定係数R2 は下記の式で求められる。
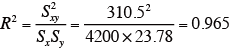
よって、重相関係数R は、
![]()
となる。
次に分散分析を行う。
全体平方和:
![]()
回帰平方和:
![]()
残差平方和:
![]()
分散分析表

分散分析の結果、危険率1%以下で回帰の要因が有意になったことから、回帰直線は、有意に当てはまるといえる。
重回帰分析
2つ以上の説明変数(X1,X2,X3,…)が目的変数y に及ぼす影響の強さや予測力を測定する。重回帰分析では、複数個の独立変数xi (i ≧ 2) と、従属変数y の間に、以下の一次式のような関係を考え、偏回帰係数b や定数a を求めるとともに、重回帰式の予測の精度を評価する。また、重回帰分析では、独立変数を固定して分析する方法(全投入法)と、独立変数を増減させて分析することで、最善の独立変数を決定するステップワイズ法がある。
![]()
ˆy : 予測値
a : 定数
bi : 偏回帰係数
i:説明変数の個数
これを解くには、
![]()
のQ を最小にするようにbi の推定値を求める。計算は、R などの統計ソフトで行う。
事例
オレンジジュースの甘味と酸味の主観的な強度が、オレンジジュースのおいしさの評価に与える影響を調べるために、20人のパネルに10種類のオレンジジュースを7段階の採点法で評価してもらったところ、各試料に対する評定値の平均が次表のようになったとする。各試料の甘味と酸味の平均評定値を独立変数、おいしさの平均評定値を従属変数として、重回帰分析することで、オレンジジュースの甘味と酸味の主観量で、おいしさの主観量が予測可能か否かを検討する。
分析結果
試料ごとの「おいしさ」「甘味」「酸味」の評定値

相関行列

分析精度

重回帰式
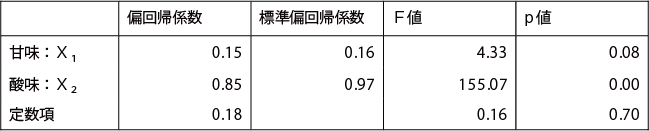
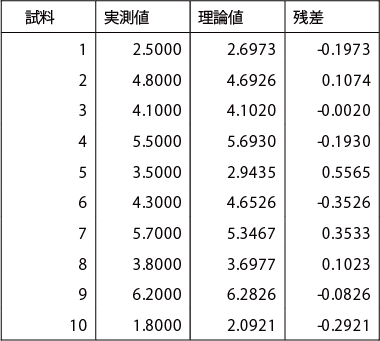
試料ごとの「おいしさ」の評定値(実測値)と回帰式による理論値
結果の解釈:
自由度修正済み決定係数が0.95 という非常に高い値を示したことから、2つの説明変数(甘味X1 と酸味X2 の主観量)で、目的変数(おいしさY)の予測ができることが示されたといえる。
得られた重回帰式は、
![]()
である。
変回帰係数を検定した結果、酸味X2 の変回帰係数が有意となった。以上から、酸味の主観量が、おいしさの評価に影響し、酸味が強いものほどおいしいと評価されることがわかる。
なお、「分析精度」を示す表にあるダーヴィンワトソン比は、系列相関の程度を表し、この値が大きいと、説明変数同士の独立性に問題があることになる。ダーヴィンワトソン比が2前後であれば、問題がないとされている。