判断分析
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
また、表示の関係から、数式が正しく表示されていない部分があります。
J-SEMS.PROで以下の解析を行うことができます。
手法
回帰分析は目的変数が数量(間隔尺度以上)であったが、判別分析法は、目的変数がカテゴリーの場合に、適用される。例えば、A群とB群に所属するデータ群が、それぞれ2 変量X1 とX2 の値を持ち、X1 とX2 の二次元の座標上にプロットされたとする。この時、A群のデータをB群に誤判別したり、B群のデータをA群に誤判別する確率を最小にする分析方法を判別分析という。
判別分析には、線形判別分析、マハラノビスの汎距離による方法、正準判別分析があるが、ここでは、線形判別法を取り上げる。
線形判別関数
2群の判別の場合
判別式は、次式で表すことができる。
![]()
最良の境界線(Z=0)の場合は、次式の直線になり、それぞれの、係数と定数項を求める。
![]()
データの全変動をST、群間変動をSB、郡内変動をSWとすると、ST = SB+SWの関係があるので、相関比(η 2=SB/ST)を最大化することで、2 群の判別精度を高めることができる。
判別分析の妥当性の評価
![]()
上記の式によりF0 値を求め、F検定を行う。
ただし、
n1:グループ1のケース数
n2:グループ2のケース数
p:変数の個数
f:n1+n2-2
D2:マハラノビスの汎距離の2乗
F表より、F(p, f-1, 0.05) もしくは、F(p, f-1, 0.01)で評価する。
F0>F ならば、良く判別できたと判断して良い。
事例
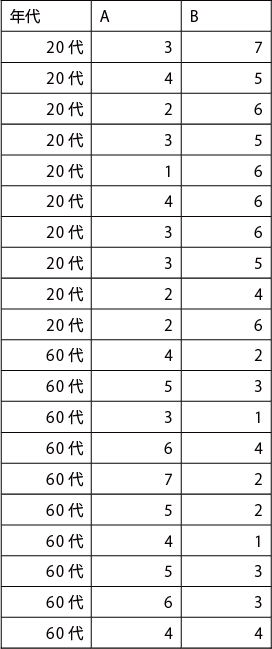
次表は、20 代と60 代の男性に2種類のスーツに対する好みの度合いを採点法で評価してもらった結果である。Rのlda 関数を用いて、これら2 種類のスーツに対する好みにより、年代を判別することが可能かをR のida 関数を用いた線形判別法で調べる。
スーツに対する好みの評価
各群の平均値
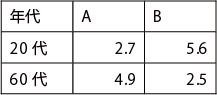
判別係数
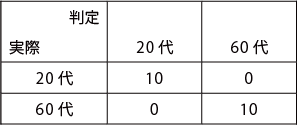
n1:10, n2:10, f:18, D2:18.31 より、F0 値は、43.24 であった(D2:マハラノビスの汎距離の2乗の求め方については、永田& 棟近(2001)を参照のこと)。
求めたF0 値43.24 は、F 表(略)の危険率1% 臨界点(F(0.01, 2, 17)= 6.11)よりも大きかったことから、判別式は、危険率1% 水準で有意となり、スーツに対する好みから年代を判別することができたといえる。
判別得点と判定結果
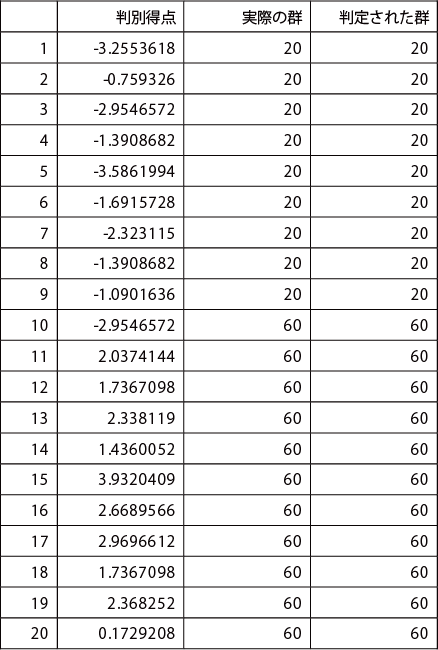
判別クラス表
