二元配置の分散分析
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
また、表示の関係から、数式が正しく表示されていない部分があります。
J-SEMS.PROで以下の解析を行うことができます。
概要
要因が2つ(例えば、試料の違いの要因と評価者の違いの要因)あったときに、それらの要因がデータに及ぼす効果について検定する。
繰り返しがない場合
10点満点の採点法で、各評価者が各試料を評価した結果を以下のような表にまとめたものを元のデータとする。
採点法によるデータ例(繰り返しがない場合)

要因A( 試料) の水準数:a=4
要因B( 評価者) の水準数:b=3
各セルの繰り返し数:r=1
以下の手順で各要因のF 値を求める。


を求める。
修正項:
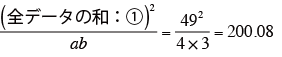
全データの2乗和:
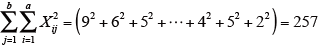
-
各変動因の平方和SS を求める。
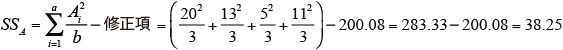
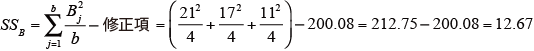

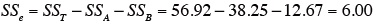
-
各変動因の自由度を求める。
要因A の自由度:dfA=a-1=3
要因B の自由度:dfB=b-1=2
誤差の自由度:dfe= (a-1) (b-1)=3 × 2=6
全体の自由度:dfT=ab-1=4 × 3-1=11 -
各要因の平均平方を求める。
MSA=SSA/dfA=38.25/3=12.75
MSB=SSB/dfB=12.67/2=6.34
MSe=SSe/dfe=6.00/6=1.00 -
各要因のF 値を求める。
FA= MSA / MSe =12.75/1.00=12.75
FB= MSB / MSe =6.34/1.00=6.34 -
F表(略)により、要因Aと要因Bの検定を行う。F表より、F(0.01,3,6)=9.7795 となるため、要因A は1% 水準で有意。また、F(0.05,2,6) =5.1433 となるため、要因B は5% 水準で有意である。
-
:分散分析表を作成する。
分散分析表

いずれの主効果も有意だったが、ここでは、試料(要因A)についてBonferroni の方法による多重比(下位検定)を行う。
試料は4つなので、比較する対の数は6になる。
最初に、下記の式によってt値を求める。
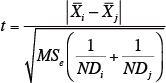
Xi :試料i の平均値
Xj :試料j の平均値
MSe:誤差の平均平方(MSe=1.00)
N:各セルの繰り返しの数(N=1)
Di, Dj:試料i, j における要因B の水準数(Di=Dj=3)
Excel 関数のT.DIST(t,dfe) 関数を使い、求めたt 値から危険率p を求め(自由度は、誤差の自由度:この例では6)、その危険率pに比較する対の数(この例では、6)を乗じた値が、求めるボンフェリーニの調整後の危険率p になる(次表)。
下位検定の結果
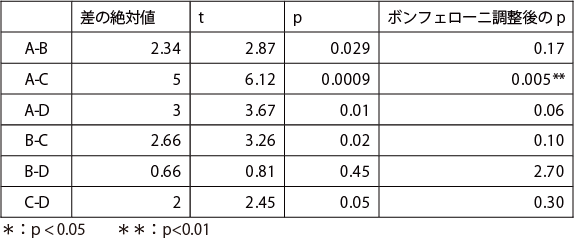
試料AとCは、ボンフェローニの調整後の危険率p が0.01 以下になったので、1%水準で有意差があるといえる。その他の組み合わせは、いずれもp>0.05 となり、有意差はなかった。
繰り返しがある場合
2要因実験で繰り返しがある場合は、各要因の母集団に含まれる水準がすべて実験に組み込まれている場合と、母集団に含まれる水準が非常に多いために、その中からサンプリングして少数の水準を実験に組み込む場合とを考える必要がある。前者の場合の分散分析モデルは母数モデルといい、後者は変量モデルという。例えば、検査したい4つの試料があり、それを3人の評価者が7段階の採点法で評価したとする(次表)。この時、4つの試料は、調べたい試料条件のすべてであるので母数モデルが適用される。一方、3名の評価者の要因については、その3名について調べたいということであれば母数モデルが適用され、たくさんいる評価者の中から3名をサンプリングして3水準としたと考えれば変量モデルが適用されることになる。そして、後者の場合は、試料の要因は母数モデル、評価者の要因は変量モデルとなることから、これを混合モデルという。ここでは、次表を両要因とも母数モデルで解析する方法と、混合モデルで解析する方法を示すことにする。
両要因とも母数モデルの場合
採点法によるデータ例(繰り返しがある場合)

上表を元にして、AB集計表(次表)を作成する。
AB集計表

要因A の水準数:m(行の数:評価者)
要因B の水準数:n(列の数:試料)
繰り返し数:r
以下の手順で各要因のF 値を求める。
-
表より、全データの2乗和を求める。
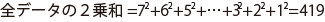
-
表より、修正項を求める。なお、要因Aの水準数m=3、要因Bの水準数n=4、各セルの繰り返し数r=2である。

-
表より、要因Aの平方和SSAを求める。
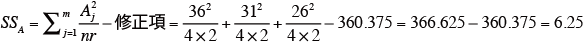
-
表より、要因Bの平方和SSBを求める。
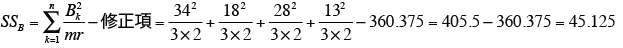
-
要因AとBの交互作用の平方和SSA× Bを求める。
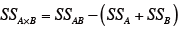
なお、SSABは、表の各要素の2乗和を繰り返し数rで割って求める。
つまり、
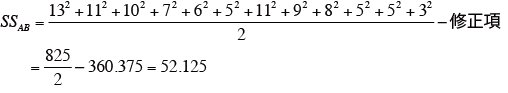
よって、
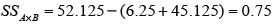
となる。 -
総平方和SST を求める。

-
誤差平方和を求める。
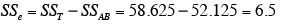
-
各変動因の自由度を求める。
要因A の自由度:dfA=m-1=2
要因B の自由度:dfB=n-1=3
交互作用A × B の自由度:df(A × B)=(m-1)(n-1)=2 × 3=6
誤差の自由度:dfe=mn(r-1)=3 × 4 × (2-1)=12
全体の自由度:dfT=mnr-1=3 × 4 × 2-1=23 -
各要因の平均平方を求める。
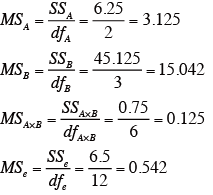
-
各要因のF値を求める。
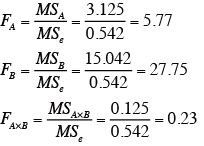
-
F表(略)より、F(2,12,0.05)=3.8853、F(3,12,0.01)=5.9526、F(6,12,0.05)=4.8206となることから、要因Aは、5%水準で、要因Bは1% 水準で有意となったが、AとBの交互作用は有意ではなかった。
-
分散分析表を作成する。
分散分析表

いずれの主効果も有意だったが、ここでは、試料についてBonferroni の方法による多重比較(下位検定)を行う。試料は4つなので、比較する対の数は6になる。
最初に、下記の式によってt値を求める。
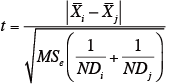
Xi :試料i の平均値
Xj :試料j の平均値
MSe:誤差の平均平方(MSe=0.54)
N:各セルの繰り返しの数(N=2)
Di, Dj:試料i, j における要因B の水準数(Di=Dj=3)
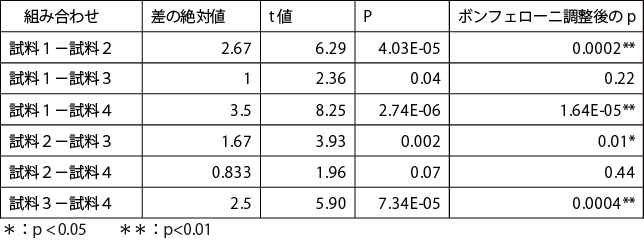
求めたt値からExcelのT.DIST(t,dfe) 関数を使い、危険率pを求め(自由度は誤差の自由度で、本事例では、12)、その危険率pに比較する対の数(この例では6)を乗じた値が、求めるボンフェローニの調整後の危険率pになる(次表)。試料2と3は、ボンフェローニ調整後の危険率pが0.5 以下になったことから、5%水準で有意な差があるといえる.同様に、試料1と2,試料1と4,試料3と4は、ボンフェローニ調整後の危険率p が0.1以下になったことから、1%水準で有意な差がある。
下位検定の結果
混合モデル
混合モデルの場合、平均平方までは、両要因が母数モデルの場合と同様で、最後のF値の求め方が異なる。各要因のF 値は、次式により求める。
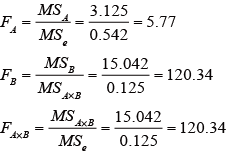
つり合い不完備型ブロック計画(BIBD)
つりあい不完備型ブロック計画においては、評価者は、t個の全試料の内、k個の試料を評価する。つまり、k<tである。k個の試料の選び方は、全試料が評価される数が等しくなるように。また、全試料を2つ一組にして選んだ時に、そのすべての可能な組み合わせの各ペアが、同人数の評価者によって評価されるようにする(下記のパラメータr の数を一定にする)。つり合い不完備型ブロック計画のパラメータは、以下の通りである。
t: 試料の数
k: 1回のセッションで一人の評価者が評価する試料の数(k<t)
b: 繰り返しp が1回の時のつり合い不完備型ブロック計画におけるブロック(評価者)の総数
r: 繰り返しp が1回の時のつり合い不完備型ブロック計画において各試料が評価される数
λ : 各試料対が同じ評価者によって評価される度数
p: 基本的なつり合い不完備型ブロック計画が繰り返される数
つり合い不完備型ブロック計画では、2要因の主効果の有意性を分散分析により検定する。つり合い不完備型ブロック計画では、正確さを増すためには、ブロック計画を繰り返して行う必要がある(繰り返しの回数p)。そこで、ブロックの総数は、p×bになる。同様に、試料毎の評価の総数は、p×rになり、各試料対が一緒に観察される総数は、p×λになる。
繰り返しpが1回の場合
要因1:評価者(ブロック数)b
要因2:試料t
分散分析表(略)
上表の分散分析表より、得られたF 値が有意であったら、下記の式により、下位検定(Fisher のLSD 検定)を行う。
![]()
t α /2,VE は、自由度VE、危険率α /2 に対応するt値。
k個のサンプルのシングルブロックをp回繰り返し評価した場合:つまり、p*b人の評価者が1回評価した場合
分散分析表(略)
F表(略)を利用して、F検定を行う。F検定の結果、有意であったら、下記の式により、下位検定(Fisher のLSD 検定)を行う。
![]()
t α /2,VEは、自由度VE、危険率α /2に対応するt値。
k個のサンプルのb個のブロックをp人の評価者が繰り返し評価した場合
分散分析表(略)
F表(略)を利用して、F検定を行う。F検定の結果、有意であったら、下記の式により、下位検定(Fisher のLSD 検定)を行う。
![]()
t α /2,VE は、自由度VE、危険率α /2 に対応するt値。
k個のサンプルのb個のブロックをp人の評価者が繰り返し評価した場合
分散分析表(略)
Excel 関数を利用して、F検定を行う。F検定の結果、有意であったら、下記の式により、下位検定(Fisher のLSD 検定)を行う。
![]()
つり合い不完備型ブロック計画BIB の例
表に、t=5,k=3,b=10,r=6,λ=3,p=1の場合の例を示す。
つり合い不完備型ブロック計画BIB の例

上表に示されたようなつり合い不完備型ブロック計画で、下表のような採点法のデータを得たとする。
採点法のデータの例
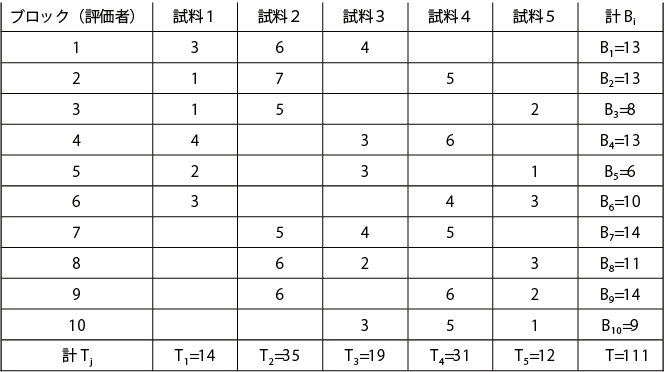
はじめにQi(i=1,5)を下記の式により求める。
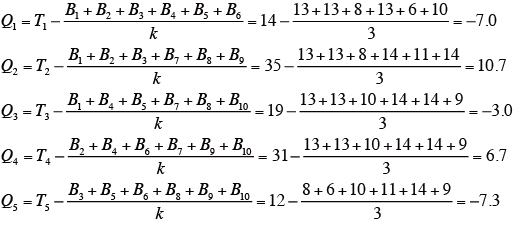
ブロック(評価者)の平方和SBを下記の式により求める。
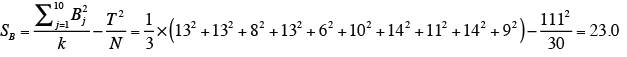
ただし、N=t × r=5 × 6=30
試料の平方和SS を下記の式により求める。
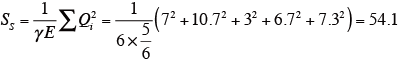
ただし、
![]()
総平方和ST を求める。
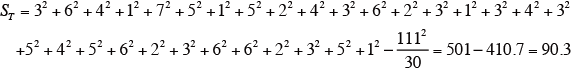
以上より、分散分析表を作成する。
分散分析表

その結果、F表(略)より、F(4,16,0.01)=4.7726 で、F0>F となり、試料の効果は1%水準で有意であった。
F検定の結果、試料の効果が有意であったので、下記の式により下位検定を行う。
![]()
α /2=0.025、VE=16 で両側検定を行う。
Excel 関数T.INV(0.025,16) より、t α /2,VE =2.12 となる。
MSE=0.825 より、
![]()
となる。
すべての組み合わせでTi とTj の差をとるとそれらは、いずれも1.22 よりも大きな値になることから、すべての試料間で5%水準で有意差がある。
なお、つり合い不完備型ブロック計画の作り方は、以下のとおりである。
ここで、
t: 試料の数
k: 1回のセッションで一人の評価者が評価する試料の数とする。
つり合い不完備型ブロック計画では、各評価者(各ブロック)は、t個の試料の中からk個の試料を測定する。
その組み合わせの数は、tCk=t!/(t-k)!k! になる。
例えば、t=5、k=3 の場合、組み合わせの数は、5!/(5-3)!3!=10 になる。繰り返しの回数(p)が1 回の時、求めた組み合わせの数がブロック数(評価者の数)になる。この10 通りの組み合わせを書きだすと表2.6.17 のようになる。A, B, C, D, Eは試料(t=5)で、そのすべての組み合わせを書き出すと、10 通りになり、それがブロック数(評価者数:b)ということになる。また、各試料が評価される回数(r)は、それぞれ6 回、一対の試料が一緒に評価される回数(λ)は、それぞれ3 回となっており、つり合いが取れている。このように、すべての組み合わせを書きだせば、自然とつり合いが取れる。
一方、ISO 29842:2011 Annex A において、t とk の組みわせが表2.6.20 の場合、評価者の数を減らすつり合い不完備型ブロック計画が提示されている。例えば、t=7、k=3 の場合、計算での組み合わせ数(パネリスト)は35 であるが、次表のように7 人のパネリストで評価することができる。
簡略化可能なtとkの組み合わせ

つり合い不完備型ブロック計画BIBDの例
