一致性の係数
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
また、表示の関係から、数式が正しく表示されていない部分があります。
手法
n人の一対比較の判断結果がどの程度一致しているかを調べて、十分に一致しているならば、n人の判断の合計順位を意味のある順位としようとするもの。
入力
- 試料数:k
- 評価者数:n
- 一対比較データ表:n人の評価者に一対比較の実験を行ない、k個の試料の中の一対の試料、例えば、試料1と試料2を比較し、試料1の方が好まれる数をデータ表の1行2列に記入する(X12)。反対に、試料2の方が好まれる数は、2行1列に記入する(X21)

解析
-
次式によってΣを計算する。
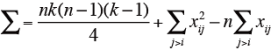
-
次式によって一致性の係数u を求める。
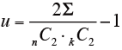
検定
- 検定表(略)のkとnの範囲内であれば、Σが表中の値以上であれば、有意となり、n人の判断が一致していると考える。
- 表にないk とn の範囲に対しては、次式により、χ 2 値、自由度df を求める。χ 20 ≧χ 2(df, α ) ならば、有意水準αで、n人の判断が一致しているといえる。

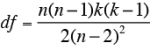
事例
5種類の洗濯機の嗜好順序を決めるために、5人のパネリストに2個ずつを対にして提示して、どちらを好むか回答させた。
その結果は、以下の表の通りである。この表には、品物jよりもi を好んだ人数が記入してある。例えば、表からは、A1 とA2 を比べて、A1 を好む人が3 人で、A2 を好む人が2 人だったことが読み取れる。

上式により、Σを求める。
なお、n=5, k=5
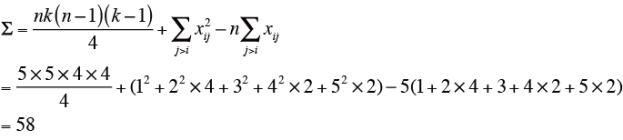
次に、uを求める。
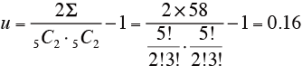
一致性係数u のΣによる検定のための表(略)より、n=5, k=5, α =5% の有意点は、Σ =60 で、Σが60 以上だと5% 水準で有意になる。今回得られたΣは58 だったので、今回得られた5人のパネリストの順位づけに一致性はあるとは言えない。