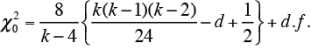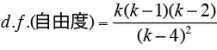一意性の係数
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
また、表示の関係から、数式が正しく表示されていない部分があります。
手法
A>B,B>CならばA>Cのはずであるが、時に、A<Cになってしまう場合がある。このような関係を一巡三角形という。試料の数がn 個あった時に、3つずつ組み合わせて一巡三角形の数dを数える場合、一巡三角形が生じる確率が十分に小さいならば、各試料間に順位をつけられた、すなわち、順位に一意性があったと考えてよい。この検定法を一意性の検定という。
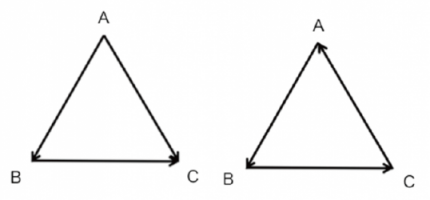
上図でA → Bは、AよりもBを好むことを示す。左の三角形は、A → B、B → C、A → Cの関係にあることから、Cが一番好まれ、次にB、最後がA という順序が一貫しており、一巡三角形ではない。
一方、右の三角形の場合は、A → B、B → C、なので、順位に一意性があるのであれば、A → Cになるはずであるのに対し、実際には、A ← Cとなってしまっており、順序関係が循環してしまっている。このような関係の三角形を一巡三角形という。
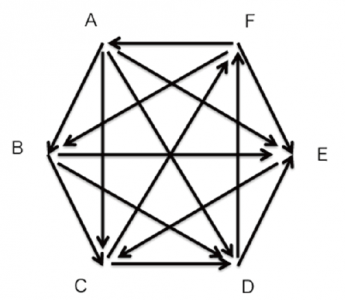
あるパネリストの評価結果:A → Bは、AよりもBの方が好きなことを示す
事例
例えば、あるパネリストが、A ~ Fの6つの飲料のパッケージのデザインに対して、一対比較法で、どちらが好きかを答えたところ、上図に示したような結果を得た。ただし、図中の矢印、A → Bは、AよりもBの方が好きなことを示すものとする。この時、6つのデザイン間に好みの順位が存在すると考えてよいだろうか。
k=6の場合は、d ≦ 1の時に、k=7の場合は、d ≦ 3の時に、5%水準で試料間に有意な順位があるといえる。k ≦ 5の時は、d=0であっても、有意に達しない。
k ≧ 8 の時は、次式によりχ 2 検定を行なう。
本事例では、k=6 で、d=6なので、試料間に有意な順位があるとはいえない。
本事例では、k=6 で、偶数なので
一巡三角形の数dを求める。図の各頂点から外に向かっている矢印の数をai とする時、dは次式によって求められる。
- 一巡三角形の数dを求める。図の各頂点から外に向かっている矢印の数をai とする時、dは次式によって求められる。
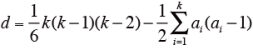
ただし、k は、試料数。
本事例では、k=6、ai、d は、下記のようになる。
a1(A):4、a2(B):3、a3(C):2、a4(D):2、a5(E):1、a6(F):3
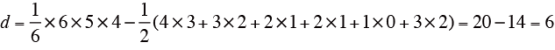
- 一意性の係数・を求める。
k が偶数のとき、
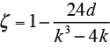
k が奇数のとき、
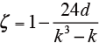
本事例では、k=6 で、偶数なので
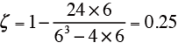
- k=6の場合は、d ≦ 1の時に、k=7の場合は、d ≦ 3の時に、5%水準で試料間に有意な順位があるといえる。k ≦ 5の時は、d=0であっても、有意に達しない。
k ≧ 8 の時は、次式によりχ 2 検定を行なう。
本事例では、k=6 で、d=6なので、試料間に有意な順位があるとはいえない。