一対比較法の手法の違い
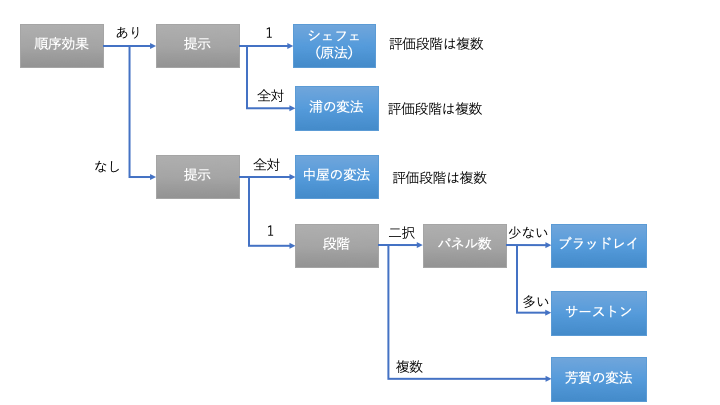
ブラッドレイ、サーストン、シェフェ(原法)、浦の変法、芳賀の変法、中屋の変法の違いは以下です。
| 手法 | 段階 | 提示 | 順序効果 |
| ブラッドレイ | 二択 | 1 | なし |
| サーストン | 二択 | 1 | なし |
| シェフェ(原法) | 複数 | 1 | あり |
| 浦の変法 | 複数 | 全対 | あり |
| 芳賀の変法 | 複数 | 1 | なし |
| 中屋の変法 | 複数 | 全対 | なし |
段階
二択
2つの試料を提示し、どちらが良い(好き)かを選択します。
例
A社の醤油ラーメンとB社の醤油ラーメン、どちらが好きですか、好きな方を選んでください。
複数
2つの試料を提示し、、どちらが良い(好き)かを段階で選択します。
例
A社の醤油ラーメンとB社の醤油ラーメン、どちらが好きですか、以下から選んでください。
- A社がとても好き
- A社が好き
- どちらでもない
- B社が好き
- B社がとても好き
提示
1
パネルに提示する試料は1組です。試料がAからDまであるとすると、各パネルには以下のように提示します。パネルは6人必要となります。
| パネル番号 | 提示 |
| 1 | 試料Aと試料B |
| 2 | 試料Aと試料C |
| 3 | 試料Aと試料D |
| 4 | 試料Bと試料C |
| 5 | 試料Bと試料D |
| 6 | 試料Cと試料D |
全対
各パネルは各試料の全ての組み合わせを評価します。試料がAからDまであるとすると、各パネルには以下のように提示します。
| パネル番号 | 提示 |
| 1 | 試料Aと試料B |
| 1 | 試料Aと試料C |
| 1 | 試料Aと試料D |
| 1 | 試料Bと試料C |
| 1 | 試料Bと試料D |
| 1 | 試料Cと試料D |
| 2 | 試料Aと試料B |
| 2 | 試料Aと試料C |
| 2 | 試料Aと試料D |
| 2 | 試料Bと試料C |
| 2 | 試料Bと試料D |
| 2 | 試料Cと試料D |
順序効果
なし
例えば、2つの飲料のパッケージのデザインについて、同時に2つ提示して比較する場合、順序の効果はないとする考え方です。
あり
2種類の食品を比較する場合、どちらを先に試食するかで評価が異なる可能性があるとする考え方です。
この場合は、試料がAからDまであるとすると、各パネルには以下のように提示します。
| パネル番号 | 提示順 |
| 1 | 試料A→試料B |
| 2 | 試料A→試料C |
| 3 | 試料A→試料D |
| 4 | 試料B→試料C |
| 5 | 試料B→試料D |
| 6 | 試料C→試料D |
| 7 | 試料B→試料A |
| 8 | 試料C→試料A |
| 9 | 試料D→試料A |
| 10 | 試料C→試料B |
| 11 | 試料D→試料B |
| 12 | 試料D→試料C |
どの手法を選ぶか
順序効果を考慮する手法(シェフェ原法)は多くのパネルが必要となります。
全対を提示する手法(浦の変法、中屋の変法)はパネルへの負担が高くなります。
書籍:「製品開発に役立つ感性・官能評価データ解析-Rを利用して-」での解説
一対比較法には、一意性の係数、一致性の係数、ブラッドレイの一対比較法、シェフェの一対比較法、サーストンの一対比較法がある。一意性の係数は、各パネリストが、すべての試料を対にして比較した時に、どの対を評価する場合でも、順序の一貫性が保たれているかどうか、判断の一次元性を示すものである。これは、パネリストごとに求める。一方、一致性の係数は、複数のパネリストが試料を対にして一対比較を行ったときに、パネリスト同士の判断結果がどれくらい一致しているのかを示すものである。
これに対し、ブラッドレイの一対比較法、シェフェの一対比較法、サーストンの一対比較法は、試料を一対比較したデータを基にして、試料の尺度化をする方法である。これらの手法は、試料を一対比較する場合に、どちらが好みの度合いや感覚の強さが強いのかを2者択一的に答えてもらうのか、あるいは、一方が他方よりもどれくらい強く感じるか、その度合いを段階評価してもらうのかによって2つに分けることができる。前者は、ブラッドレイの一対比較法とサーストンの一対比較法が該当し、後者は、シェフェの一対比較法が該当する。パネルが、一対の試料の強さの違いを数量で評価できそうな場合は、シェッフェの方法やその変法を用いるが、二者択一的な判断しかできそうもない場合は、ブラッドレイの方法かサーストンの方法を用いる。また、サーストンの方法では、反復数が少ないと尺度値が安定しないため、反復数(もしくは、パネル数)が、最低30 はほしいところである。ブラッドレイの方法の場合は、反復数が少なくても分析可能である。