一元配置の分散分析

書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。

また、表示の関係から、数式が正しく表示されていない部分があります。
J-SEMS.PROで以下の解析を行うことができます。

概要

3つ以上の試料に対する評価についての母集団の平均値に差はないという帰無仮説を検定する場合に用いる。例えば、4つの試料に関して調べるとき、その中の一つの試料に対する評価値は、4つの試料の平均評価値からのずれ（群間のずれ）とその試料の平均からのずれ（群内のずれ）に分解できる。群間のずれは、試料の性質の違いによって生じるずれであるのに対し、群内のずれは、同一の試料内で生じるものであり、誤差によって生じると考えられる。
そこで、群間と群内のずれの大きさを比較し、群内のずれの大きさ（誤差）に較べて、群間のずれの大きさが相対的に大きければ、試料の性質の違いが測定値の違いとしてあらわれたことを示すものと考えようというのが分散分析の基本的な考え方である。

分散分析の前提条件

1)各水準の内側でのデータの分布が、正規分布に近いこと（正規性）
2) 各水準の内側でのデータの分散が、大体同じであること（等分散性）
なお、等分散性の検定は、バートレット検定を行う。バートレット検定で等分散性が否定された場合は、分散分析を行わず、順位検定のクラスカル・ウォリスH 検定で検定する。

例題

ある製品のパッケージデザインの試作品が4つある。試作品ごとに4名ずつのグループを作り、これらの試作品の良さを、10点満点の採点法で評定した時、以下の表のような結果を得た。4つのパッケージデザインに対する評定値に差があるといえるか。また、差があった場合、どのパッケージ間に差があるか。

試料の数：k=4
繰り返しの数：n=4

パッケージデザインの評価結果

以下の数値を計算してF 値を求め、検定する。

修正項を求める。
総平方和SST を求める。
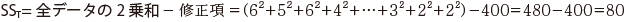
試料の要因（群間）の平方和SSA を求める
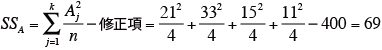
群内の平方和SSe を求める。
SSE=SST-SSA=80-69=11
各要因の自由度を求める。
群間の自由度：dfA=k-1=3
郡内（誤差）の自由度：dfe=k(n － 1)=4 × 3=12
全体の自由度：dfT=nk － 1=4 × 4 － 1=15
群間と群内の平均平方を求める。
MSA=SSA/dfA=69/3=23.0
MSe=SSe/dfe=11/12=0.92
試料の要因（群間）のF0 値を求める。
F0= MSA / MSe =23.0/0.92=25.0
分散分析表を作成する。
F表（略）より、1% 水準でdfA=3、dfe=12 に対応するF 値は、2.6055 である。F0=25.0 であることから、F0>F となり、試料の要因は1% 水準で有意である。

分散分析表

試料の要因についてBonferroniの方法による多重比較（下位検定）を行う。
はじめに試料の対ごとに評価値の平均の差についてt検定を行う。試料は4つなので、比較する対の数は6になる。t値は、下記の式によって求める。

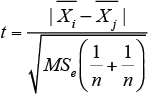
Xi ：試料i の平均値
Xj ：試料j の平均値
MSe：誤差の平均平方
n：繰り返しの数

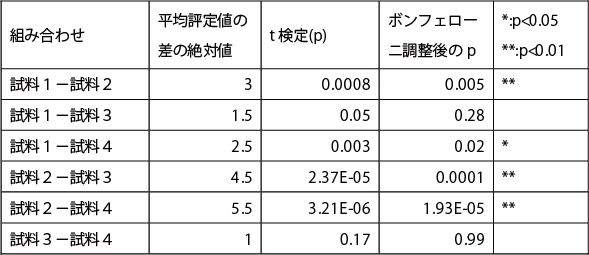
上記の式によって求めたｔ値と誤差の自由度dfe を用いて、例えば、ExcelのT.DIST.2T(t, dfe)により危険率pを求める。求めたpに比較する組み合わせの数（今回は6）を乗じた値が、ボンフェローニの修正後の危険率になる（次表）。
次表、試料1と2、試料2と3、試料2と4の間に1%水準で、試料1と4の間に5%水準で有意差があった。

下位検定の結果

感性・官能評価システム J-SEMS