ページの検定
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
事例
p個の試料の順位をn人のパネルが評価したとき(下表)、あらかじめ想定した順位通りであったかどうかを検定する。
各サンプルの順位データ
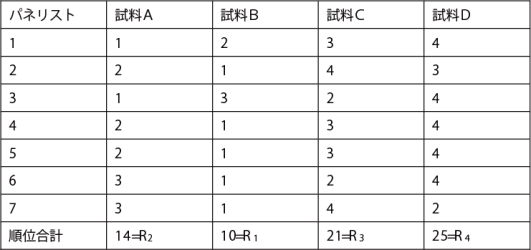
H0(帰無仮説): 理論的な順位和をΓ i とすると、Γ 1= Γ 2= Γ 3=…= Γ p
H1(対立仮説): Γ 1< Γ 2< Γ 3<…< Γ p
Page の係数 L=R1 + 2R2 + 3R3 + …+pRp
表のデータ例 L=10 + 2 × 14 + 3 × 21 + 4 × 25 = 201
検定表(略)の試料数pと評価者数jに対応するLの値と、計算した値を比べて、計算した値が対応する表の値よりも大きければ、帰無仮説は棄却され、対立仮説が採用される。つまり、試料の順位は、想定した順位通りになっていることになる。
今回の例では、試料数4,評価者数7なので、5%水準では、表中の値は、189、1%水準では、193 になる。
計算で得られた値は、L=201 なので、1%水準で有意ということになり、帰無仮説は棄却される。