ブラッドレイの一対比較法
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
また、表示の関係から、数式が正しく表示されていない部分があります。
J-SEMS.PROで以下の解析を行うことができます。
手法
どちらが良いか(あるいは、好きか)という1か0の評価データから、判定比を逐次近似により推定する方法。ブラッドレイは、試料j よりも試料i の方が良い(好きだ)と答える確率をπ ij としたときに、π ij は、試料i とj の判定比π i 及びπ j から、以下の式で求められると考えた。即ち、
![]()
ブラッドレイの一対比較法は、この確率を基にして、各試料の判定比π i を推定しようとするものである。なお、π i の推定値は、次の連立方程式を解くことによって求められる。
![]()
![]()
なお、kは試料の数、nは反復数である。
また、fiは、資料i が、iを除くすべての試料との組み合わせで、iの方が良い(好きだ)と答えた数の総和である。
実例
判定結果一覧表

- 試料数をk、比較回数をnとする。上表の例では、k=4、n=5である。
まず、Ai を他の(k-1) 個の試料とn 回比較したn(k-1) の判定の中でAi が良いと判断された回数fi を求める。
その手順としては、まず各組み合わせで○の数を求め、その結果を以下の表にまとめる。下の表の1行目のA1と2列目のA2の位置には、A1 とA2 で、A1の方が良い(あるいは、好き)と判断された回数(この場合は、2)が書かれている。同様に、2行目のA2と1列目のA1の位置には、A1とA2で、A2の方が良い(あるいは、好き)と判断された回数(この場合は、3)が書かれている。以下、同様である。そして、この表の各行の和が、fi になる。

-
判定比を以下の逐次近似により推定する。
1)第0次近似の求め方
処理間に差がないと仮定して、

今回の例では、
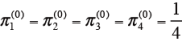
と置く。2)第1次近似π (1) の求め方
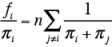
より、
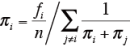
よって、
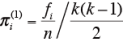
今回の例では、
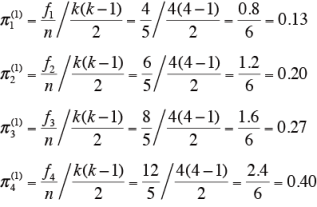
となる。
また、
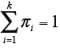
より、求めたπ i(1) をの全体の和が1になるように調整する。
つまり、
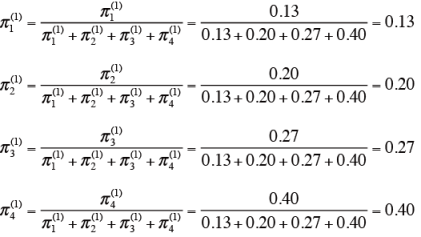
3)第2次近似
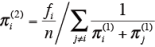
より、
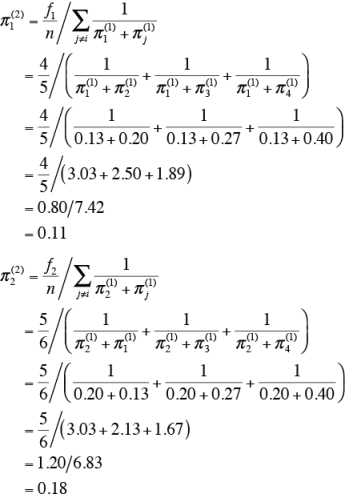
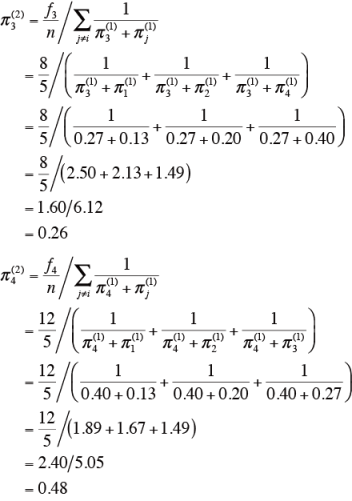
となる。
また、
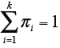
より、求めたπ i(1) を全体の和が1になるように調整する。
つまり、

3)以下、同じ操作を繰り返して、各判定比が収束するまでn+1 次の判定比を求める。
4)このようにして判定比が求められたら、試料間に差があるかどうかを検定する。以下の式により、自由度k-1のχ 2 検定を行う。得られたχ 2 値が、χ 2 分布の5%点以下であれば、試料間に有意差があるといえる。
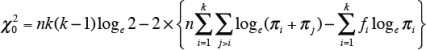
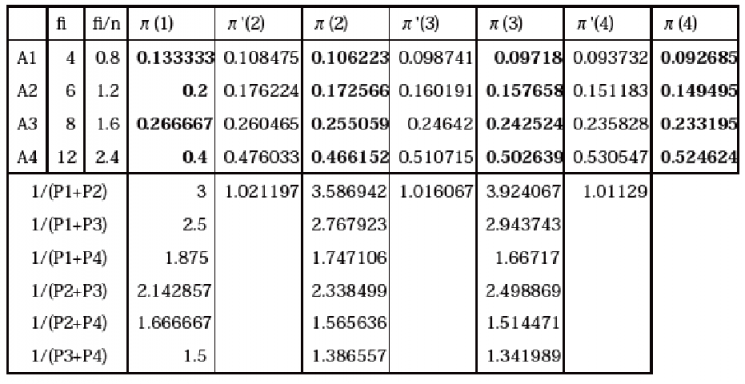
以上の手順で、第4次近似までの判定比を、下表に示す(太い文字が各回の判定比である)
得られた判定比
ここでは、4次近似で得られた判定比を最終的な判定比の推定量とする。
つまり、
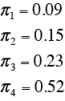
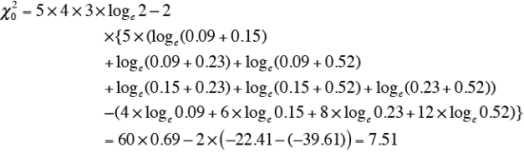
![]()
結論
得られたχ 2 値(7.51)は、自由度3のχ 2 の5%点の値(7.81)よりも小さな値だったことから、試料間に有意差があるといえない。