フリードマンの順位検定
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
また、表示の関係から、数式が正しく表示されていない部分があります。
手法
各試料に対して複数のパネリストが行なった順位づけのデータをもとにして(各試料の順位和をもとにして)、試料間の順位に差があるかどうかを検定する。完備型とつりあい不完備型実験計画による分析方法がある。
完備型ブロック計画
手順
順位データ

フリードマン検定の棄却限界値(Ftest 値)を求める。
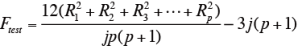
Ri:試料i の順位和
j:評価者数
p:試料の数
Ftest 値が、検定表(略) の棄却限界値以上であれば、危険率5%、もしくは、1%で、試料間に順位の差があると判定する。試料数や評定者数が多く、表に載っていない場合は、得られたFtest 値を自由度p-1のχ 2 値とみなし、 χ 2 検定を行う。χ 2 検定は、Excel 関数CHIDIST(Ftest, p-1) により危険率を求め、その値が、0.05 以下であれば、5%水準で有意、0.01 以下であれば、1%水準で有意となる。
同順位があった場合
F値の代わりにF’ を下記の式により、求める
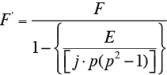
ただし、
![]()
n1,n2,…..,nk は、同順位の各グループの数を示す。
例えば、下表でいえば、パネリスト2とパネリスト4で同順位が見られた。パネリスト2は、2つの試料を同順位としたので、n1=2とする。パネリスト4は、3つの試料を同順位としたので、n2=3である。そこで、E=(23-2)+(33-3)=6+24=30である。
求めたEを上式に代入してF’を求め、表(略)より、検定する。試料数やパネルの数が多く、表(略)に載っていない場合は、得られたF値を自由度p-1 のχ 2 値とみなし、χ 2 検定を行う。χ 2 検定は、Excel 関数CHIDIST(F’, p-1) により危険率を求め、その値が、0.05 以下であれば、5%水準で有意、0.01 以下であれば、1%水準で有意となる。

各サンプルの順位データ
下位検定
Ftest 値による検定、あるいは、χ 2 検定で有意の場合に、下位検定を行う。
![]()
ここで、有意水準を個別のペアではなく、実験全体で5%( α ) に設定するので、個々のペアの有意水準( α ’)は
![]()
となり、例えば、α =0.05, p=5 の時、上式より、α ’=0.005 となる。そして、α ’=0.005 に対応するZ 値は、両側検定なので、正規分布表(略)より求める(Z0.0025=2.81になる)。
事例
12 名の評価者に車体の色の好みについて順位法で尋ねたところ、表2.2.12 のような回答を得た。この結果から、車体の色の好みに差があるかどうか検定した。
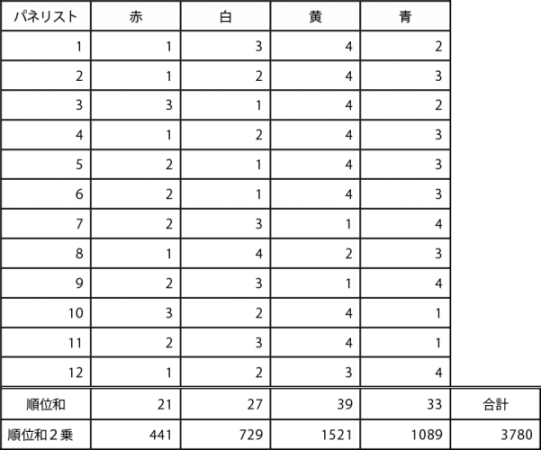
順位法サンプルデータ
考え方
計算例
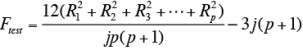
Ri:試料i の順位和
j:パネルの数
p:試料の数
j=12, p=4 を上の式に代入したところ、Ftest値は、9.0になった。
表(略)より、j=12, p=4 の5% 棄却域は、7.70、1% 棄却域は、10.68である。よって、危険率5%水準で、車体の色の好みに差があるといえる。
次に下位検定を行い、LSDを求めたところ、16.69になった。順位和の差が16.69 以上あるのは、赤と黄であり、赤と黄の間に有意な差があった。
つり合い不完備型ブロック計画
手順

つり合い不完備型ブロック計画サンプルデータ
フリードマン検定の棄却限界値(Ftest 値)を求める。
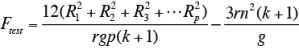
Ri:試料i の順位和
j:評価者数
k:各評価者が評価する試料の数
p:試料数 n:各試料が評価される回数
r:繰り返し数
g:1対の試料が一緒に評価される回数
Ftest 値が、表(略)の棄却限界値以上であれば、危険率5%、もしくは、1%で、試料間に順位の差があると判定する。試料数や評定者数が多く、表(略)に載っていない場合は、得られたFtest 値を自由度p-1のχ 2 値とみなし、χ 2 検定を行う。検定は、Excel 関数CHIDIST(Ftest, p-1) により危険率を求め、その値が、0.05 以下であれば、5%水準で有意、0.01 以下であれば、1%水準で有意となる。この例では、j=10, p=5, r=1, k=3, n=6, g=3 である。Ftest 値は、下記のようになる。
![]()
表(略)より、j=10, p=5の5%棄却域は、9.25、1%棄却域は、12.38である。よって、危険率5%水準で、試料間に差がある。
下位検定
Ftest 値による検定、あるいは、χ 2 検定で有意の場合に、下位検定を行う。
![]()
ここで、有意水準を個別のペアではなく、実験全体で5%( α ) に設定するので、個々のペアの有意水準( α ’)は
![]()
となり、例えば、α =0.05, p=5の時、上式より、α ’=0.005となる。そして、α ’=0.005 に対応するZ 値は、両側検定なので、Excel 関数のNORMSINV( α ‘/2) で計算して求める(z=NORMSINV (0.0025)=2.81 になる)。
そこで、求めるLSD は、以下のようになる。
![]()
順位和Ri の差が8.88以上のペアは、試料Dと試料Eのペアのみ(差は、9.0)であったことから、下位検定の結果、試料Dと試料Eとの間に5%水準で有意な差がある。