スピアマンの順位相関係数
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
手法
順位相関は、順序尺度データで与えられる2変数同士や、パネリスト同士の相関の程度を示すもので、スピアマンの順位相関係数では、2つの特性それぞれに順位がつけられた時、その順位値をそのまま計量値とみなして、相関係数を計算する。
入力:パネリスト同士の相関を求める場合
データ例

片側検定(+か−のいずれかの値しかとらないことがわかっている)か両側検定(+と−の値をとる可能性がある)かに注意する必要がある。
同順位がある場合は、平均順位をつける。
同順位がない場合
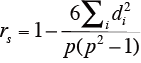
rs: スピアマンの順位相関係数
p: 試料の数
d: 試料i に関して、2つの順位の差
同順位がある場合
パネリスト1(あるいは変数1)がk箇所にt1,t2,…,tk 個, パネリスト2(あるいは変数2)が1箇所にu1,u2,…,ul 個の同順位を持つときは、同順位のものには平均順位を与え、rs は、次式を用いる。
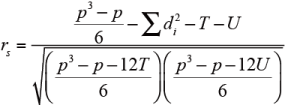
なお、
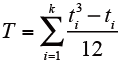
ti はパネリスト1(あるいは変数1)の広がりを示し、kはタイの数を示す。
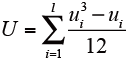
ui はパネリスト2(あるいは変数2)の広がりを示し、lはタイの数を示す。
検定
表(略)より、片側検定の場合:Σ di2 が表の値以下であれば、有意水準αで有意。
両側検定の場合:Σ di2 もしくは、(p3-p)/3-Σ di2 のいずれかが表の値以下であれば、有意水準αで有意。
p ≦ 10 のとき:表中の値をそのまま利用する。
p > 10 のとき:正規分布による近似を用いる。Σ di2 が下記の式によって求めた値よりも小さければ、
有意水準αで有意になる。
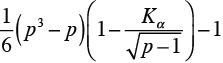
なお、K αの値は、表(略) を参照のこと。
事例
二人のパネリストに6 種類の電気カミソリの使用感の良さについて、順位付けをしてもらい、二人のパネリストの評価の関連性の度合いを、順位相関を求めることで調べた。データは、上の表の通り。
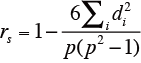
より、rs=0.77 (Σ di2 =8.0,p=6)
今回は両側検定を行う。検定表より、p=6 の時、両側検定でΣ di2 が4 以下であれば、5%水準で有意であるが、8.5 であったので、有意ではない。