シェフェの一対比較法(原法)
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
また、表示の関係から、数式が正しく表示されていない部分があります。
J-SEMS.PROで以下の解析を行うことができます。
手法
評点をつける一対比較法。評定者は、試料に対する嗜好を評価する検査で、一対の試料を提示された時に、どちらの試料の方が好ましいかを答えるのと同時に、それがどれくらい好ましいかを評定する。t個の試料の中から任意の一組について、総勢N人の評定者に1 回ずつ評点をつける一対比較法で評価してもらう(原法)。各組の評定者の数は、n=N/{t(t-1)} 人となる。各評定者は、1回ずつしか評定しないので、多くの評定者を必要とする。比較的規模の大きい評価研究に向いている。
試料の数:t
全評価者の人数:N
各グループの評価者の人数:n(n=N/{t(t-1)} )
実例
Ai がAj よりも非常によいと思ったら +2点
Ai がAj よりもいくぶんよいと思ったら + 1 点
Ai がAj とまったく差がないと思ったら 0 点
Ai がAj よりもいくぶん悪いと思ったら − 1 点
Ai がAj よりも非常に悪いと思ったら − 2 点
n人の評価者のうち、1番目の評価者が、t個の試料の中からiを先に、jを後にした順序で比較したときの評点をxijl とする。その時のデータ構造は、
![]()
となる。
ここで、
α i, α j:試料i、試料j の平均嗜好度
γ ij:組み合わせの効果
δ ij:順序効果
eijl:誤差
評点の度数表
評点の度数表の例を以下に示す。
評点の度数表(この例は、t=4、N=144、n=12)
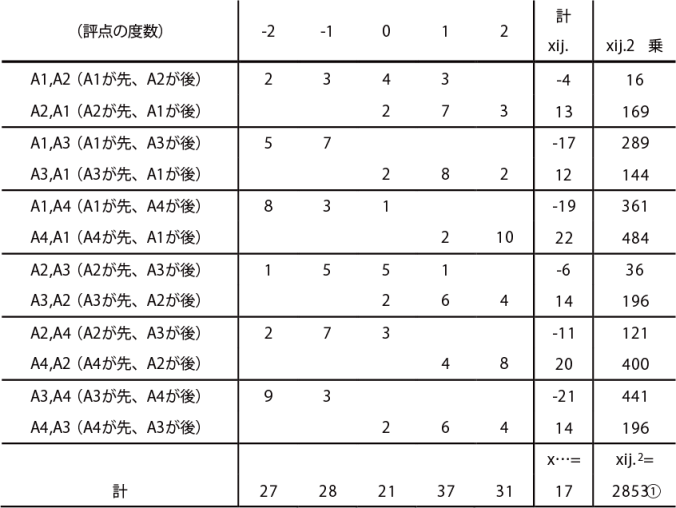
平均嗜好度α i の推定値
平均嗜好度を求める手順は以下の通りである。
- 上の表で求めた各組み合わせにおける嗜好度の合計値を表に写し取り(表2.3.8)、行和(Xi..)と列和(X.i.)を求める。
- 対応する行和と列和の差(Xi..-X.i.)を求める。
- 以下の式より、平均嗜好度(α i)を求める。

平均嗜好度を求めるための計算表

嗜好度(主効果)の分散Sα
嗜好度(主効果)の分散Sαは、下記の式により求める。
![]()
組み合わせ効果
組み合わせ効果の分散S γは、下記の式により求める。
![]()
組み合わせ効果の分散を求めるための計算表

組み合わせ効果の推定値( γ ij)
組み合わせ効果の推定値( γ ij) は、以下の式によって求める。
![]()
組み合わせ効果の推定値を求めるための計算表
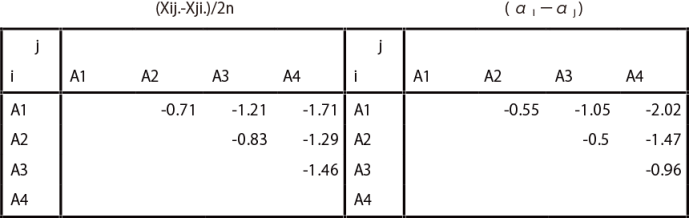
組み合わせ効果の推定値γ ij=(Xij.-Xji.)/2n − ( α i −α j )

順序効果
順序効果(δ ij)の分散は、以下の式によって求める。
![]()
順序効果の分散を求めるための計算表

順序効果(δ ij)の推定値
順序効果(δ ij)の推定値は、下記の式により求める。
![]()
順序効果の推定値を求めるための計算表

総平方和
![]()
誤差平方和
![]()
分散分析表

検定は、Excel 関数 F.DIST.RT(F値, 各効果の自由度, 誤差の自由度) により危険率(p値)を求めるか、F表を用いて行う。
下位検定
ヤードスティックY0.05、Y0.01 を求める。

なお、ステューデントのq の値は、表2.3.16a, bから求める。また、σ 2 は、分散分析表の誤差の不偏分散の値(この例では、0.45)である。
すべての対について、下位検定を実施する。
試料間の嗜好度の差
試料間の差を求める(下表)。試料間の嗜好度の差が、求めたY0.05、Y0.01 よりも値が大きければ、5%水準、あるいは、1%水準で有意差がある。
試料間の嗜好度の差
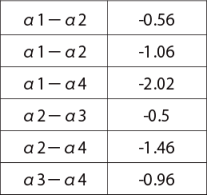
ここで、
σ 2 = 0.45
q(4,132,0.05) = 3.68
q(4,132,0.01) = 4.50
なお、ステューデントのqについては、誤差の自由度132に該当する値が表(略)になかったために、自由度120、試料数4に該当する値を採用する。
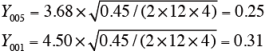
上表より,試料間の嗜好度の差の絶対値は、いずれも0.31 以上なので、すべての試料間の評定値に1%水準で有意差がある。