シェフェの一対比較法（中屋の変法）

書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。

また、表示の関係から、数式が正しく表示されていない部分があります。
J-SEMS.PROで以下の解析を行うことができます。

手法

比較順序は考えず、かつ、一人の評価者がすべての組み合わせを1 回ずつ比較する場合に用いる（中屋の変法）。この方法も、浦の変法と同様に、小規模に実験をしたい時に便利な方法である。この方法は、浦の変法と同様に、一人の評価者がすべての組み合わせを評価するが、一対の試料を提示する際に、時間的な順序や空間的な位置の効果が、データには影響しないという前提で、比較順序を考慮しないので、試行数は、浦の変法の半分になる。

例

試料の数：t=4
評価者の数：N=3

試料iとjの組み合わせに対して、評価者ｌの評定結果を表に記入する（次表）。すべての条件が終わったら、行列の対角線の反対側の半分は空白になっているはずであるので、その対応する部分に、得られたデータの符号を逆にした数値を記入し、表を完成させる。試料毎の評点の合計Σ Xi.l と評点の2 乗和Σ Xi.l2 も求めておく。
各評価者の評定結果
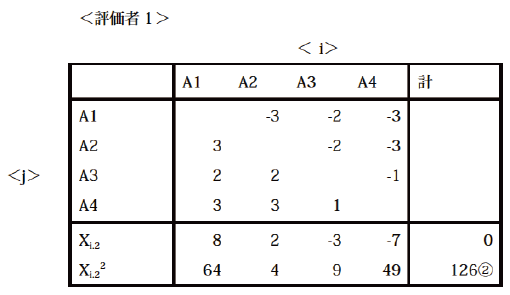
評価者全員の評点の合計についても、同様にまとめる。
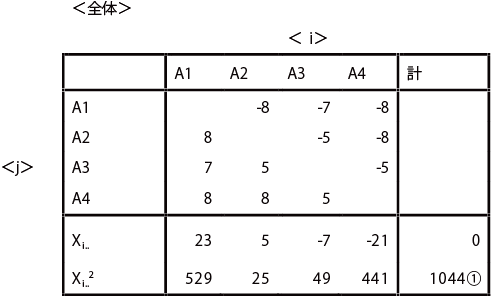
平均嗜好度と嗜好度の個人差を下記の式により求める。
平均嗜好度

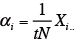
嗜好度の個人差

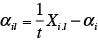
組み合わせの効果

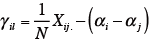
平均嗜好度の推定値

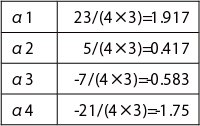
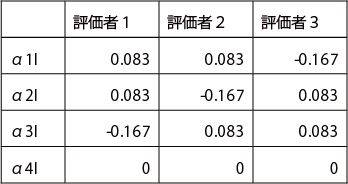
平均嗜好度の個人差の推定値
組み合わせ効果を求める。
1)Xij./N を求める

2)α i ｰα j を求める

3)組み合わせ効果　γ ij=Xij./N − ( α i ｰα j) を求める
各効果の平方和

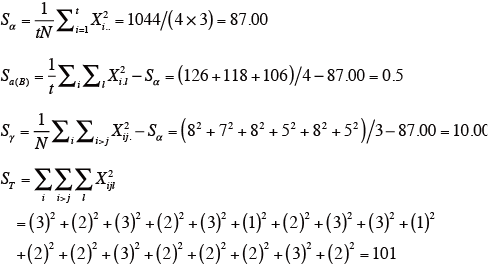
※ ST は、得られたデータの総平方和。

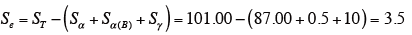
分散分析表
下位検定
すべての対について、下位検定を実施する。試料間の嗜好度の差は、上表に示すとおりである。
次式より，ヤードスティックY0.05、Y0.01 を求める。

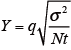
q：ステューデントのq
なお、ステューデントのq の値は、表（略）から求める。

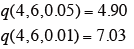
σ 2：分散分析表の誤差の不偏分散の値: この例では0.58
N=3
t=4
試料間の嗜好度の差が、求めたY0.05、Y0.01 よりも値が大きければ、5％水準、あるいは、1％水準で有意差がある。