サーストンの一対比較法

書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
詳しくはこちら
また、表示の関係から、数式が正しく表示されていない部分があります。
J-SEMS.PROで以下の解析を行うことができます。
詳しくはこちら

手法

ブラッドレイの方法と同様に、対にした2 種類の試料のどちらが上位かを判定するだけで、シェフェの方法のように、その程度まで答えさせることはしない。サーストンの一対比較法の基になるモデルは、サーストンの比較判断の法則である。例えば、試料iと試料jを一対比較する場合を考える。試料iが与えられた時、試料iによって評価者が感じる主観的な大きさは、いつも一定とは限らず、ばらつきを持つ。そのばらづきは、平均値がXi、標準偏差がσ iの正規分布になると考える。同様に、試料jが与えられた時には、その主観的な大きさは、平均値がXj、標準偏差がσ jの正規分布になると考える。かりに試料i に対する主観的な大きさの平均値Xi が、試料j に対するそれよりも大きかったとするならば、試料iの分布は、試料jのそれよりも、主観的な大きさの尺度上で、右に位置することになる。しかし、試料iの分布と試料jの分布が完全には離れていなくて、重なっていた場合に問題になるのは、平均値はiの方が高くても、iとjを比較した時に、いつもi の方が大きく感じるということはないということである。それぞれは、正規分布にしたがってばらつきがあるので、時には、その関係が逆転することもある。両者を比較する時に、評価者がiの方がjよりも大きいと感じるのは、両者の主観的な大きさの差、つまり、Ri-Rj が0よりも大きい（正の）値を取った時ということになる。そこで、試料iと試料jに対する主観的な大きさの差の値を考えた時、その値は、すでに述べたように正の値を取ることもあれば、負の値を取ることもあり、その主観的な大きさの差の分布は、平均値が、Ri − Rj 、標準偏差が、

の正規分布になると考える。
これが、サーストンの比較判断の法則である。これを図で示すと、以下のようになる。

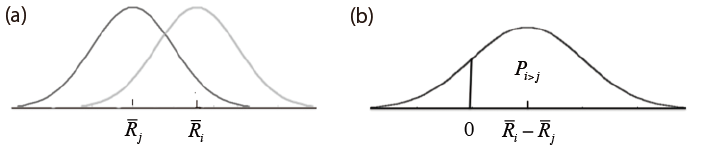
一対比較法の原理
(a) 試料i と試料j に対する主観的大きさの分布     (b) 試料i と試料j に対する主観的大きさの差の分布

ここで、 iとjを一対比較させた時に、iの方が大きい（あるいは、好きだ）と答える確率は、Ri ｰRj が0よりも大きい（正の）値を取る確率ということになるので、上図左の横軸の0から伸びた垂線と正規関数で囲まれた面積に対応する。そして、この0から、差の分布の平均値Ri − Rj までの距離Ri − Rj を、差の分布の標準偏差

を単位にした距離で表すと、

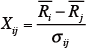
となり、

となる。

サーストンの一対比較法では、σ iとσ jが異なる値を取るか、同じ値を取るか、iとjの相関係数を0と考えるか否かなどで、5つのケースを考えているが、この中で、最も実用的で一般的に用いられているのは、ケースⅤである。ケースⅤでは、σ iとσ jは同じ値を取り、rij=0 と仮定する。
すると、

となる。
ここで、iとjの差の単位を√2σ とすれば、

となる。

解析法

大根を切った時の5種類の包丁の切れ味について、サーストンの一対比較法により調べた。5種類の包丁を対にすると5C2=10 組の対ができる。そこで、300人の消費者を30人ずつの10組に分け、どちらの包丁の方が切れ味が良いかを評価してもらった。
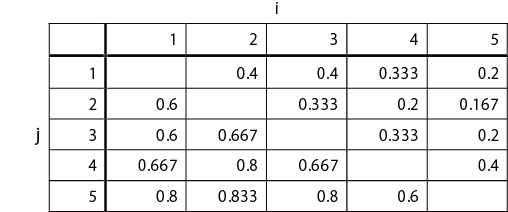
結果は、以下の表のようになった。なお、この表は、包丁i が包丁j よりも切れ味がよいと判断された数を示している。

i>j の度数

次に、上記の度数をもとにして、包丁i が包丁j よりも切れ味が良いと判断された比率を求めると、以下の表になる。

i>j の比率Pi>j

i>j の比率をＺ変換することで、対毎にRi – Rjを求める。Z変換は、正規分布表（略）を用いて変換する。

Zi>j=Ri − Rj

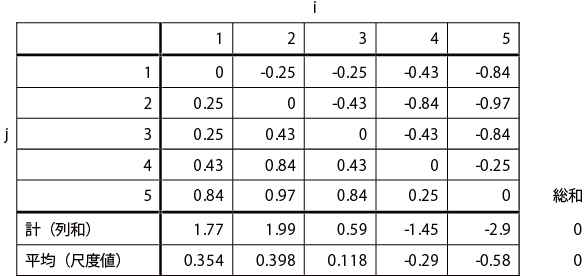
次に、同じ表で列毎に列和を求め、さらに平均を求める。この平均値が、各試料の尺度値になる。なお、各列の列和の合計と、平均値の合計が０になることを確認する。

内的整合性の検定

得られた尺度値の一次元性をチェックするために、内的整合性の検定を下記の手順で行う。

1. 得られた尺度値から、Ri– Rj の期待値ˆZi> j を計算する。

   ˆZi> j = Ri − Rj
   
   

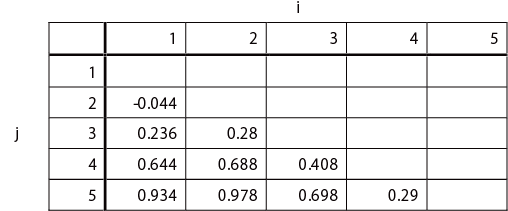
2. Zi>j の期待値（ˆZ i> j ）から比率の期待値ˆpi> j を求める。

   比率の期待値ˆpi> j
   

3. 比率の実測値Pi>j と期待値とˆpi> j の食い違いをみるために、それぞれの比率を逆正弦変換する。
   変換式は、下記の通り。
   

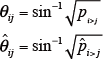
   θの実測値θ ij
   

   　θの期待値ˆθij
   

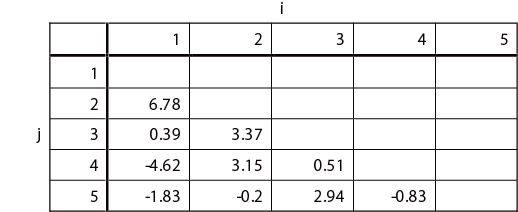
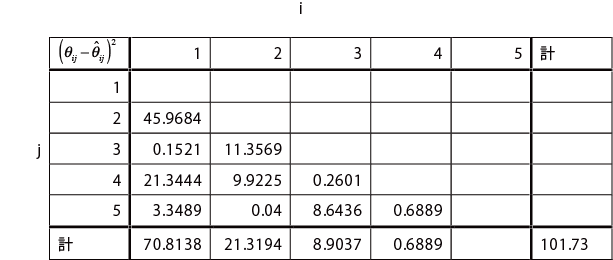
4. θ ij とˆθij の差の平方和（総和）を求める。

   θij −ˆθij の差
   
   

   θ ij とˆθij の差の平方和

   

5. χ２値を求める。
   
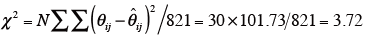
   なお、Nは各対を判断した評価者の人数で、今回は30。
   
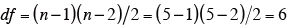
   n は、試料の数。

   χ 2 表（略）より、危険率(p) 0.05、自由度df=6の時のχ２は、12.592であることから、p>0.05となるので、実測値と期待値の間には、統計的に有意な差はないことになり、内的整合性が確認されたといえる。