ケンドールの一致性係数

書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
詳しくはこちら
また、表示の関係から、数式が正しく表示されていない部分があります。

J-SEMS.PROで以下の解析を行うことができます。
詳しくはこちら

手法

n個の試料をk人の評価者に順位づけさせたときに、k人の評価者の評定結果にどの程度の共通性があるかを示す指標である。

順位データ表

1. 1. 各試料の順位の和を求め、Sj とする（上表）
   2. 順位の和の残差平方和S を求める。
      

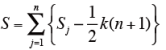
   3. 一致性係数Wを計算する。
      

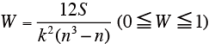
   4. W の有意性を検定する。
      １）n≦ 7, k ≦ 20 のときは、検定表（略）を用いる。
      Sの実測値が、表の値以上であれば、有意である（一致性がある）と判断する。

      ２）表にないnとkに対しては、χ 2 検定を行う。χ 2 表（略）より
      
      が、自由度n － 1 のχ 2 値よりも大きければ（χ 20> χ 2 (n-1, α ) 有意である。

      ３）同順位がある場合は、同順位のものに平均順位を与え、同順位のない場合と同様にして各試料の順位の和、S1, S2, S3, …., Sn 及び、その残差平方和S を計算する。
      各評価者（各行）のl 箇所にそれぞれt1,t2,t3,…..,tl 個の同位の広がりがあるとき
      
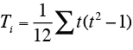
      を求め、さらに、その合計Σ Ti を求める。
      Ｗは、次式により求める。
      

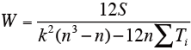
有意性の検定は、次式のχ 02 が自由度n-1 のχ 2 分布に近似的に従うことを用いる。すなわち、χ 20> χ 2 (n-1, α ) ならば、有意である。

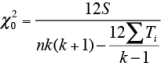
事例

A社製の3種類の車に対する乗り心地について10名の評価者に順位を付けてもらったら、下記の表のようなデータが得られた。10名の評価者の評価に一致性があるといえるか。

サンプルデータ

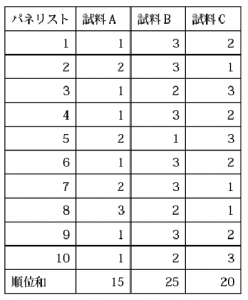
試料の数n=3、評価者の数k=10 より、

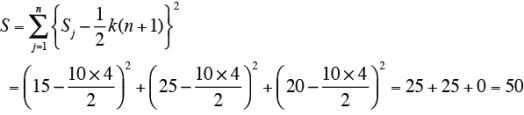
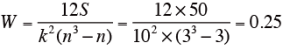
となる。
検定表（略）よりn=3、k=10のSの5％有意点は、60.0で、求めたSはその値よりも小さいため、評価者の評価の一致性は低く、統計的に有意な一致性があるとはいえない。