クラスカル-ウォリスのH検定
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
以下の例の手順および数値の詳細は書籍でご確認ください。
また、表示の関係から、数式が正しく表示されていない部分があります。
手法
ウィルコクソンの順位和検定は、2種類の順位の差を検定するものであったが、これを3種類以上の順位の差を検定するように拡張したもの。
k組の試料につけられた順位を次のように表す。ただし、各組の試料の数は、ni (i=1,2,…..,k) とする。
第1組:R11, R12, …, R1n1
第2組:R21, R22, … R2n2
…
第i 組:Ri1, Ri2, …, Rini
…
第k組:Rk1, Rk2, …, Rknk
Rij:第i 組の中のj 番目の試料につけられた順位。
ni:各組の試料数。
k:組の数。
事例
A社、B社、C社製のビジネススーツの着心地の良さを比較するために、一人のパネリストにA社のスーツを5 着、B社のスーツを6 着、C社のスーツを5 着着てもらい、着心地の良い物から順位をつけさせた。
A の順位:1, 3, 4, 7, 8
B の順位:2, 5, 9, 10, 11, 15
C の順位:6, 12, 13, 14, 16
- 各組ごとの順位和Ti を次式によって求める。
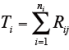
T1=23
T2=52
T3=61 -
試料の総数Nを次式によって求める。
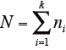
N=16 -
試料の総数Nを次式によって求める。
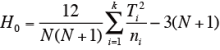
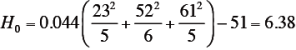
- 検定
k=3 あるいは、k=4 で、n1, n2, n3, (n4) が表2.2.18 に記載されている範囲にあるときは、H0 が表中の限界値(H)以上であれば、5%水準で有意である。
この例では、得られたH0 6.38 は、付表で示されたk=3, n1=5, n2=5, n3=6 の有意点、H:5.7294 よりも大きな値を取ったことから、5%水準で有意であり、A社、B社、C社のスーツの着心地には、差があるといえる。
表(略)に記載されていないk, n1, n2, n3, (n4) に対しては、自由度k-1 のχ 2 値と比較して、H0 ≧χ 2(k-1, 0.05) ならば、有意(帰無仮説を捨てる)。Excel 関数を用いて計算する場合は、H0 が、Excel関数CHIINV(k-1, 0.05) で求めた値よりも大きければ、5% 水準で有意。 - 同順位がある場合
同順位のものには、平均順位を与え、H0 を次式によって求める。
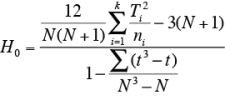
ここで、tは、タイ(同順位)の広がりの大きさである。
そして、χ 2 表(略)よりH0 ≧χ 2(k-1, 0.05) ならば有意(帰無仮説を捨てる)。