ウィルコクソンの順位和検定
書籍「製品開発に役立つ感性・官能評価データ解析−Rを利用して−」より引用
検定表、数表は省略しています。
また、表示の関係から、数式が正しく表示されていない部分があります。
以下の例の手順および数値の詳細は書籍でご確認ください。
手法
m個のAとn個のBをこみにして順位をつけたとき、AとBの2組の順位付けに差があるかどうかを検定したいときに用いる。
Aの数がm個あるとき、Aにつけることのできる順位の組み合わせは、m+nCm通りある。ここで、Aの順位和をTとすると、Aの様々な組み合わせに応じてTの確率分布を求めることができる。このようにして、Aの数mと、Bの数nが与えられたときに、順位和Tの分布を計算し、「AとBの分布の中心位置に差がない」という帰無仮説を検定する。実際の検定は、検定表を用いる。
事例
2種類のエンジンAとBの加速時の騒音の大きさの比較を行った。あるパネリストが騒音が小さいものから順位をつけたところ、下表のような結果になった。エンジンAとBの騒音に違いがあるといえるであろうか。
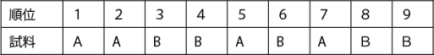
データ例
m:Aの個数 4
n:Bの個数 5
m≦nとする。
解析法
Aのもつ順位Ri を求める。 Ri: R1, R2, R3, ….., Rm である。
TとT’のうち、小さい方を表2.2.17 の限界値と比較して、それが限界値以下であれば、5%水準で有意であり、帰無仮説を棄却する。
両側検定で、m=4, n=5 の時の限界値は、11。T=15>11 なので、帰無仮説は棄却できず、エンジンAとBの騒音の大きさに違いがあるとはいえない。
片側検定の場合、u0 ≧ u0.05=1.645 であれば、有意。
両側検定の場合、u0 ≧ u0.025=1.960 であれば、有意。
ただし、T は、試料Aの順位和である。
mとnが大きくて、付表にない場合には、下記の式により、正規化近似を行って検定する。
また、下記の式より、T’ を求める。
- 「2組の順位付けには差がない」という帰無仮説をたてる。
両側検定の場合:対立仮説は、「2組の順位付けには差がある」
片側検定の場合:対立仮説は、「Aの方がBよりも良い」あるいは、「Aの方がBよりも悪い」
以上の仮説を立てて検定する。なお、今回は両側検定とする。 - Aのもつ順位Ri を求める。 Ri: R1, R2, R3, ….., Rm である。
- Aのもつ順位和Tを求める。
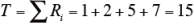
また、下記の式より、T’ を求める。

- TとT’のうち、小さい方を表(略)の限界値と比較して、それが限界値以下であれば、5%水準で有意であり、帰無仮説を棄却する。
両側検定で、m=4, n=5 の時の限界値は、11。T=15>11 なので、帰無仮説は棄却できず、エンジンAとBの騒音の大きさに違いがあるとはいえない。
mとnが大きくて、付表(略)にない場合には、下記の式により、正規化近似を行って検定する。
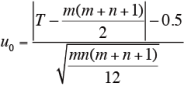
片側検定の場合、u0 ≧ u0.05=1.645 であれば、有意。
両側検定の場合、u0 ≧ u0.025=1.960 であれば、有意。
ただし、T は、試料Aの順位和である。
同順位がある場合
同順位のものには平均順位を与える。AとBをこみにして1箇所にそれぞれ、t1, t2, ….. , tl 個の同順位の広がりがあるとき、下記の式により、u0 を求め、正規分布によって検定する。
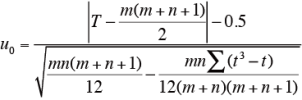
片側検定の場合、u0 ≧ u0.05=1.645 であれば、有意。
両側検定の場合、u0 ≧ u0.025=1.960 であれば、有意。